设椭圆C1的方程为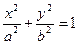 (a>b>0),曲线C2的方程为y=
(a>b>0),曲线C2的方程为y=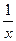 ,且曲线C1与C2在第一象限内只有一个公共点P.
,且曲线C1与C2在第一象限内只有一个公共点P.
(1)试用a表示点P的坐标;
(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;
(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个. 设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式.
.在直角坐标平面中,△ABC的两个顶点为 A(0,-1),B(0, 1)平面内两点G、M同时满足① ,②
,② =
= 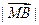 =
=  ③
③ ∥
∥
(1)求顶点C的轨迹E的方程
(2)设P、Q、R、N都在曲线E上 ,定点F的坐标为( , 0) ,已知
, 0) ,已知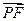 ∥
∥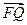 ,
, 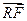 ∥
∥ 且
且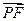 ·
·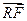 = 0.求四边形PRQN面积S的最大值和最小值.
= 0.求四边形PRQN面积S的最大值和最小值.
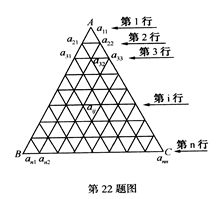
.如图,把正三角形ABC分成有限个全等的小正三角形,且在每个小三角形的顶点上都放置一个非零实数,使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等.设点A为第一行,…,BC为第n行,记点A上的数为a ,…第i行中第j个数为a
,…第i行中第j个数为a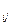 (1≤j≤i).若a
(1≤j≤i).若a =
=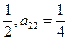
(1)求a
(2)试归纳出第n行中第m个数a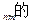 表达式(用含n,m的式子表示,不必证明);
表达式(用含n,m的式子表示,不必证明);
(3)记S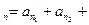 …+a
…+a ,证明:n≤
,证明:n≤ +
+ +…+
+…+ ≤
≤
设函数f ( x ) = 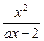 (a ÎN*), 又存在非零自然数m, 使得f (m ) =" m" ,
(a ÎN*), 又存在非零自然数m, 使得f (m ) =" m" ,
f (– m ) < – 成立.
成立.
(1) 求函数f ( x )的表达式;
(2) 设{an}是各项非零的数列, 若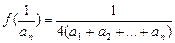 对任意nÎN*成立, 求数列{an}的一个通项公式;
对任意nÎN*成立, 求数列{an}的一个通项公式;
在(2)的条件下, 数列{an}是否惟一确定? 请给出判断, 并予以证明.
.设函数y=f(x)的定义域为(0,+∞),且对任意的正实数x, y,均有
f(xy)=f(x)+f(y)恒成立.已知f(2)=1,且当x>1时,f(x)>0。
(1)求f(1), f(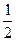 )的值;
)的值;
(2)试判断y=f(x)在(0,+∞)上的单调性,并加以证明;
(3)一个各项均为正数的数列{an}满足f(Sn)=f(an)+f(an+1)-1,n∈N*,其中Sn是数列{an}的前n项和,求数列{an}的通项公式;
(4)在(3)的条件下,是否存在正数M,使2n·a1·a2…an≥M· .(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
.(2a1-1)·(2a2-1)…(2an-1)对于一切n∈N*均成立?若存在,求出M的范围;若不存在,请说明理由.
.已知二次函数 经过点(0,10),其导数
经过点(0,10),其导数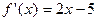 ,当
,当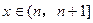 (
(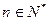 )时,
)时,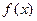 是整数的个数记为
是整数的个数记为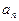 。
。
(1)求数列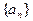 的通项公式;
的通项公式;
(2)令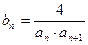 ,求数列
,求数列 的前n项(
的前n项(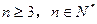 )项和
)项和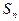 。
。