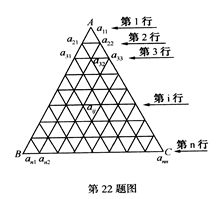
.如图,把正三角形ABC分成有限个全等的小正三角形,且在每个小三角形的顶点上都放置一个非零实数,使得任意两个相邻的小三角形组成的菱形的两组相对顶点上实数的乘积相等.设点A为第一行,…,BC为第n行,记点A上的数为a ,…第i行中第j个数为a
,…第i行中第j个数为a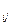 (1≤j≤i).若a
(1≤j≤i).若a =
=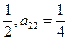
(1)求a
(2)试归纳出第n行中第m个数a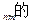 表达式(用含n,m的式子表示,不必证明);
表达式(用含n,m的式子表示,不必证明);
(3)记S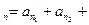 …+a
…+a ,证明:n≤
,证明:n≤ +
+ +…+
+…+ ≤
≤
已知函数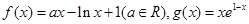 。
。
(1)求函数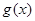 在区间
在区间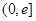 上的值域;
上的值域;
(2)是否存在实数a,对任意给定的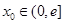 ,在区间
,在区间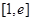 上都存在两个不同的
上都存在两个不同的 ,使得
,使得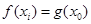 成立.若存在,求出a的取值范围;若不存在,请说明理由.
成立.若存在,求出a的取值范围;若不存在,请说明理由.
在数列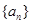 中,
中,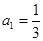 ,且前n项的算术平均数等于第n项的
,且前n项的算术平均数等于第n项的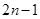 倍(
倍(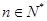 ).
).
(1)写出此数列的前5项;
(2)归纳猜想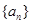 的通项公式,并用数学归纳法证明.
的通项公式,并用数学归纳法证明.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落,小球在下落过程中,将3次遇到黑色障碍物,最后落入A袋或B袋中。已知小球每次遇到黑色障碍物时向左、右两边下落的概率都是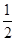 .
.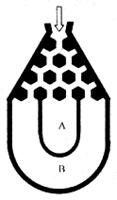
(1)求小球落入A袋中的概率P(A);
(2)在容器入口处依次放入4个小球,记X为落入A袋中小球的个数,试求X=3的概率和X的数学期望EX.
已知 是二次函数,方程
是二次函数,方程 有两个相等的实数根,且
有两个相等的实数根,且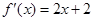 。
。
(1)求 的表达式;
的表达式;
(2)若直线 把
把 的图象与两坐标轴围成的图形面积二等分,求t的值.
的图象与两坐标轴围成的图形面积二等分,求t的值.
已知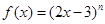 展开式的二项式系数和为512,且
展开式的二项式系数和为512,且
 .
.
求 的值;(2)求
的值;(2)求 的值.
的值.