如图,在△ABC中,在AC上取点N,使得AN= AC,在AB上取点M,使得AM=
AC,在AB上取点M,使得AM= AB,在BN的延长线上取点P,使得NP=
AB,在BN的延长线上取点P,使得NP= BN,在CM的延长线上取一点Q,使MQ=λCM时,
BN,在CM的延长线上取一点Q,使MQ=λCM时,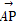 =
=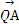 ,试确定λ的值.
,试确定λ的值.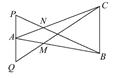
若函数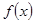 满足下列条件:在定义域内存在
满足下列条件:在定义域内存在 使得
使得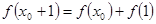 成立,则称函数
成立,则称函数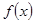 具有性质
具有性质 ;反之,若
;反之,若 不存在,则称函数
不存在,则称函数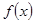 不具有性质
不具有性质 .
.
(1)证明:函数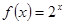 具有性质
具有性质 ,并求出对应的
,并求出对应的 的值;
的值;
(2)已知函数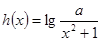 具有性质
具有性质 ,求
,求 的取值范围;
的取值范围;
(3)试探究形如① 、②
、② 、③
、③ 、④
、④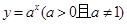 、⑤
、⑤ 的函数,指出哪些函数一定具有性质
的函数,指出哪些函数一定具有性质 ?并加以证明.
?并加以证明.
已知a>0且a≠1,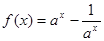 。
。
(1)判断函数f(x)是否有零点,若有求出零点;
(2)判断函数f(x)的奇偶性;
(3)讨论f(x)的单调性并用单调性定义证明。
已知A、B两城相距100km,在两地之间距A城 km处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数
km处D地建一核电站给A、B两城供电,为保证城市安全.核电站距市距离不得少于10km.已知供电费用与供电距离的平方和供电量之积成正比,比例系数 .若A城供电量为20亿度/月,B城为10亿度/月.
.若A城供电量为20亿度/月,B城为10亿度/月.
(1)把月供电总费用 表示成
表示成 的函数,并求定义域;
的函数,并求定义域;
(2)核电站建在距A城多远,才能使供电费用最小.
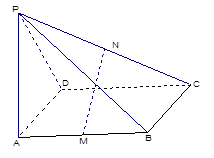
如图,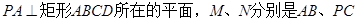 的中点.
的中点.
(1)求证: ;
;
(2)求证: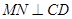 ;
;
若非零函数 对任意实数
对任意实数 均有¦(a+b)=¦(a)·¦(b),且当
均有¦(a+b)=¦(a)·¦(b),且当 时,
时, .
.
(1)求证: ;
;
(2)求证: 为减函数;
为减函数;
(3)当 时,解不等式
时,解不等式