过椭圆Γ: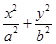 =1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为
=1(a>b>0)右焦点F2的直线交椭圆于A,B两点,F1为其左焦点,已知△AF1B的周长为8,椭圆的离心率为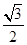 .
.
(1)求椭圆Γ的方程;
(2)是否存在圆心在原点的圆,使得该圆的任意一条切线与椭圆Γ恒有两个交点P,Q,且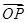 ⊥
⊥ ?若存在,求出该圆的方程;若不存在,请说明理由.
?若存在,求出该圆的方程;若不存在,请说明理由.
设函数
.
(1)当
时,求
的单调区间;
(2)若
在
上的最大值为
,求
的值.
某迷宫有三个通道,进入迷宫的每个人都要经过一个智能门,首次到达此门,系统会随机(即等可能)为你打开一个通道.若是1号通道,则需要1小时走出迷宫;若是2号、3号通道,则分别需要2小时、3小时返回智能门.再次到达智能门时,系统会随机打开一个你未到过的通道,直至走出迷宫为止.令
表示走出迷宫所需的时间.
(1)求
的分布列;
(2)求
的数学期望.
已知函数
.
(1)当
时,求
在区间
上的取值范围;
(2)当
时,
,求
的值.
设函数
=
+
.
(Ⅰ)画出函数
的图像:
(Ⅱ)若不等式
的解集非空,求
的取值范围.
已知直线 : , :
(当
时,求
与
的交点坐标,
过坐标原点O做
的垂线,垂足为
、
为
的中点,当
变化时。