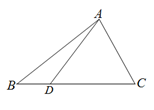
已知等比数列{an}满足an+1+an=9·2n-1,n∈N*.
(1)求数列{an}的通项公式;
(2)设数列{an}的前n项和为Sn,若不等式Sn>kan-2对一切n∈N*恒成立,求实数k的取值范围.
(本小题满分10分)设命题p:函数 的定义域为R, 命题q:双曲线
的定义域为R, 命题q:双曲线 的离心率
的离心率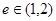 ,
,
(1)如果p是真命题,求实数 的取值范围;
的取值范围;
(2)如果命题“p或q”为真命题,且“p且q”为假命题,求实数 的取值范围.
的取值范围.
已知等差数列 满足
满足 ;数列
;数列 的前n项和为
的前n项和为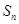 ,且满足
,且满足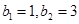 ,
,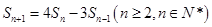 .
.
(Ⅰ)分别求数列 的通项公式;
的通项公式;
(Ⅱ)若对任意的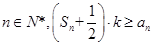 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
在 中,角
中,角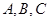 所对的边分别为
所对的边分别为 ,且
,且 .
.
(Ⅰ)当 时,求证:
时,求证: ;
;
(Ⅱ)若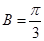 ,
,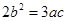 ,求
,求 的值
的值
如图,某小区拟在空地上建一个占地面积为 平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为
平方米的矩形休闲广场,按照设计要求,休闲广场中间有两个完全相同的矩形绿化区域,周边及绿化区域之间是道路(图中阴影部分),道路的宽度均为 米.怎样设计矩形休闲广场的长和宽,才能使绿化区域的总面积最大?并求出其最大面积.
米.怎样设计矩形休闲广场的长和宽,才能使绿化区域的总面积最大?并求出其最大面积.
如图,△ABC中, .求AC的长.
.求AC的长.