如图,多面体ABC-A1B1C1中,三角形ABC是边长为4的正三角形,AA1∥BB1∥CC1,AA1⊥平面ABC,AA1=BB1=2CC1=4.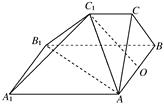
(1)若O是AB的中点,求证:OC1⊥A1B1;
(2)在线段AB1上是否存在一点D,使得CD∥平面A1B1C1,若存在,确定点D的位置;若不存在,请说明理由.
(本小题满分12分)
甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在8,9,10环,且每次射击击中与否互不影响.甲、乙射击命中环数的概率如下表:
| 8环 |
9环 |
10环 |
|
| 甲 |
0.2 |
0.45 |
0.35 |
| 乙 |
0.25 |
0.4 |
0.35 |
(I)若甲、乙两运动员各射击1次,求甲运动员击中8环且乙运动员击中9环的概率;
(II)若甲、乙两运动员各自射击2次,求这4次射击中恰有3次击中9环以上(含9环)的概率.
(本小题满分12分)
一个口袋巾装有标号为1,2,3的6个小球,其中标号1的小球有1个,标号2的小球有2个,标号3的小球有3个,现从口袋中随机摸出2个小球.
(I)求摸出2个小球标号之和为3的概率;
(II)求摸出2个小球标号之和为偶数的概率;
(III)用 表示摸出2个小球的标号之和,写出
表示摸出2个小球的标号之和,写出 的分布列,并求
的分布列,并求 的数学期望
的数学期望 .
.
某人的一张银行卡的密码共有6位数字,每位数字都可以从0~9中任选一个,他在银行的自动提款机上取钱时,忘记了密码的最后一位数字,求:
(I)任意按最后一位数字,不超过2次就按对的概率.
(II)如果他记得密码的最后一位是偶数,不超过2次就按对的概率.
.将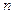 件不同的产品排成一排,若其中
件不同的产品排成一排,若其中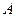 ,
,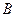 两件产品排在一起的不同排法有48种,则
两件产品排在一起的不同排法有48种,则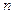 =.
=.
如图,棱锥P—ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=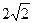 .
.
(1)求点C到平面PBD的距离; (2)在线段
(2)在线段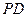 上是否存在一点
上是否存在一点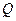 ,使
,使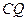 与平面
与平面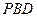 所成的角的正弦值为
所成的角的正弦值为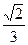 ,若存在,
,若存在,
指出点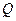 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.