(14分)一般认为激光器发出的是频率为ν的“单色光”．实际上它的频率并不是真正单一的．激光频率ν是它的中心频率，它所包含的频率范围是Δν(也称频率宽度)．如图所示，让单色光照射到薄膜表面a，一部分光从前表面反射回来(这部分光称为甲光)，其余的光进入薄膜内部，其中的一小部分光从薄膜后表面b反射回来，再从前表面折射出(这部分光称为乙光)，甲、乙这两部分光相遇叠加而发生干涉，称为薄膜干涉，乙光与甲光相比，要在薄膜中多传播一小段时间Δt.理论和实践都证明，能观察到明显稳定的干涉现象的条件是：Δt的最大值Δtm与Δν的乘积近似等于1，即只有满足Δtm·Δν≈1才会观察到明显稳定的干涉现象．
已知某红宝石激光器发出的激光频率ν＝4.32×1014 Hz，它的频率宽度Δν＝8.0×109 Hz.让这束激光由空气斜射到折射率n＝
的薄膜表面，入射时与薄膜表面成45°角，如图所示．
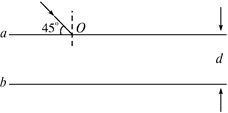
(1)求从O点射入薄膜中的光的传播方向及速率．
(2)估算在如图所示的情况下，能观察到明显稳定干涉现象的薄膜的最大厚度dm.
如图所示，在光滑平直轨道上有A、B、C三个物体，物体A、B均向右匀速运动，物体B的速度速度vB= 4.0m/s，B先与C碰撞，碰撞后B、C分离，之后B再与A碰撞粘在一起共同运动，且最后三个物体具有相同的速度v =2m/s，已知A的质量mA = 2kg，B的质量mB = 2kg，C的质量mC = 3kg．求：
① B与C碰撞后B的速度；
② 碰前A的速度vA；
③ 整个过程中，系统由于碰撞产生的内能．
如图所示，为玻璃材料制成的一棱镜的截面图，一细光束从圆弧AB的中点E点沿半径射入棱镜后，恰好在圆心O点发生全反射，经CD面反射，再从圆弧的F点射出，已知，OA=a，OD=
．求:
①出射光线与法线夹角的正弦值
②光在棱镜中传播的时间．
如图所示，有两个不计质量的活塞M、N将两部分理想气体封闭在绝热气缸内，温度均是270C．M活塞是导热的，N活塞是绝热的，均可沿气缸无摩擦地滑动，已知活塞的横截面积均为S=2cm2，初始时M活塞相对于底部的高度为Ｈ=27cm，N活塞相对于底部的高度为h=18cm．现将一质量为m=400g的小物体放在M活塞的上表面上，活塞下降．已知大气压强为p0=1.0×105Pa, 
①求下部分气体的压强多大；
②现通过加热丝对下部分气体进行缓慢加热，使下部分气体的温度变为1270C，求稳定后活塞M、N距离底部的高度．
如图所示，两条平行的金属导轨相距L = lm，金属导轨的倾斜部分与水平方向的夹角为37°，整个装置处在竖直向下的匀强磁场中．金属棒MN和PQ的质量均为m=0.2kg，电阻分别为RMN =1Ω和RPQ =" 2Ω" ．MN置于水平导轨上，与水平导轨间的动摩擦因数μ=0.5，PQ置于光滑的倾斜导轨上，两根金属棒均与导轨垂直且接触良好．从t=0时刻起，MN棒在水平外力F1的作用下由静止开始以a =1m/s2的加速度向右做匀加速直线运动，PQ则在平行于斜面方向的力F2作用下保持静止状态．t=3s时，PQ棒消耗的电功率为8W，不计导轨的电阻，水平导轨足够长，MN始终在水平导轨上运动．求：
（1）磁感应强度B的大小；
（2）t=0～3 s时间内通过MN棒的电荷量；
（3）求t =6s时F2的大小和方向；
（4）若改变F1的作用规律，使MN棒的运动速度v与位移s满足关系：
，PQ棒仍然静止在倾斜轨道上．求MN棒从静止开始到s=5m的过程中，系统产生的热量．
如图所示，一质量为m的物块在与水平方向成θ的力F的作用下从A点由静止开始沿水平直轨道运动，到B点后撤去力F， 物体飞出后越过“壕沟”落在平台EG段．已知物块的质量m =1kg，物块与水平直轨道间的动摩擦因数为μ=0.5，AB段长L=10m，BE的高度差h =0.8m，BE的水平距离 x =1.6m．若物块可看做质点，空气阻力不计，g取10m/s2．
（1）要越过壕沟，求物块在B点最小速度v的大小；
（2）若θ=370，为使物块恰好越过“壕沟”，求拉力F的大小；
（3）若θ大小不确定，为使物块恰好越过“壕沟”，求力F的最小值（结果可保留根号）．