如图所示,质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动,星球A和B两者中心之间距离为L.已知A、B的中心和O三点始终共线,A和B分别在O的两侧.引力常数为G.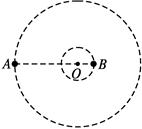
(1)求两星球做圆周运动的周期.
(2)在地月系统中,若忽略其他星球的影响,可以将月球和地球看成上述星球A和B,月球绕其轨道中心运行的周期记为T1.但在近似处理问题时,常常认为月球是绕地心做圆周运动的,这样算得的运行周期为T2.已知地球和月球的质量分别为5.98×1024 kg和7.35×1022 kg.求T2与T1两者平方之比.(结果保留三位小数)
如图所示,两块相同平板
、
置于光滑水平面上,质量均为
。
的右端固定一轻质弹簧,左端
与弹簧的自由端
相距
。物体
置于
的最右端,质量为
且可以看作质点。
与
以共同速度
向右运动,与静止的
发生碰撞,碰撞时间极短,碰撞后
与
粘连在一起,
压缩弹簧后被弹回并停在A点(弹簧始终在弹性限度内)。
与
之间的动摩擦因数为
,求:
(1) 、 刚碰完时的共同速度 和 的最终速度 ;
(2)此过程中弹簧最大压缩量 和相应的弹性势能 。
如图甲所示,空间存在一范围足够大的垂直于
平面向外的匀强磁场,磁感应强度大小为
。让质量为
,电荷量为
的粒子从坐标原点
沿
平面以不同的初速度大小和方向入射到磁场中。不计重力和粒子间的影响。
(1)若粒子以初速度
沿
轴正向入射,恰好能经过
轴上的
点,求
的大小;
(2)已知一粒子的初速度大小为
,为使该粒子能经过
点,其入射角
(粒子初速度与
轴正向的夹角)有几个?并求出对应的
值;
(3)如图乙,若在此空间再加入沿
轴正向、大小为
的匀强电场,一粒子从
点以初速度
沿
轴正向发射。研究表明:粒子在
平面内做周期性运动,且在任一时刻,粒子速度的
分量
与其所在位置的
坐标成正比,比例系数与场强大小
无关。求该粒子运动过程中的最大速度值
。
质量为
、长为
的杆水平放置,杆两端
、
系着长为3
的不可伸长且光滑的柔软绳,绳上套着一质量为
的小铁环。已知重力加速度为
,不计空气影响。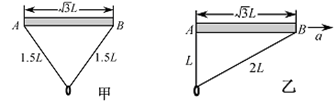
(1)现让杆和环均静止悬挂在空中,如图甲,求绳中拉力的大小;
(2)若杆与环保持相对静止,在空中沿
方向水平向右做匀加速直线运动,此时环恰好悬于
端的正下方,如图乙所示。
①求此状态下杆的加速度大小
;
②为保持这种状态需在杆上施加一个多大的外力,方向如何?
如图所示,一不可伸长的轻绳上端悬挂于
点,下端系一质量
的小球。现将小球拉到
点(保持绳绷直)由静止释放,当它经过
点时绳恰好被拉断,小球平抛后落在水平地面上的
点。地面上的D点与
在同一竖直线上,已知绳长
,
点离地高度
,
、
两点的高度差
,重力加速度
取
,不计空气阻力影响,求:
(1)地面上 两点间的距离 ;
(2)轻绳所受的最大拉力大小。
如图所示,O点离地面高度为H,以O点为圆心,制作一个半径为R的四分之一光滑圆弧轨道,小球从与O点等高的圆弧最高点A从静止滚下,并从B点水平抛出,试求:
(1)小球落地点到O点的水平距离.
(2)要使这一距离最大,应满足什么条件?最大距离为多少?