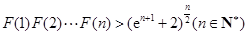如图甲,△ABC是边长为6的等边三角形,E,D分别为AB、AC靠近B、C的三等分点,点G为BC边的中点.线段AG交线段ED于F点,将△AED沿ED翻折,使平面AED⊥平面BCDE,连接AB、AC、AG形成如图乙所示的几何体。
(1)求证BC⊥平面AFG;
(2)求二面角B-AE-D的余弦值.
(本小题共14分)如图,四边形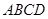 与
与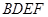 均为菱形,
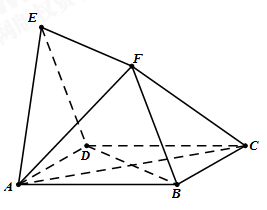
均为菱形, 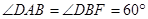 ,且
,且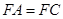 .
.
(Ⅰ)求证: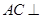 平面
平面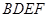 ;
;
(Ⅱ)求证: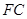 ∥平面
∥平面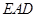 ;
;
(Ⅲ)求二面角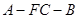 的余弦值.
的余弦值.
(本小题共13分)已知函数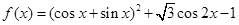 .
.
(1)求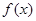 的最小正周期和图象的对称轴方程;
的最小正周期和图象的对称轴方程;
(2)求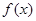 在区间
在区间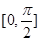 上的最大值和最小值.
上的最大值和最小值.
(本小题满分13分)设函数f(x)=x3–3ax2+3bx的图象与直线12x+y–1=0相切于点(1,–11).
(1)求a,b的值;
(2)求函数f (x)的单调区间.
(本小题共13分)如图,在四棱锥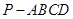 中,底面
中,底面 是矩形,
是矩形, 分别是
分别是 的中点,
的中点, 平面
平面 ,且
,且 ,
, .
.
(Ⅰ)证明: 平面
平面 ;
;
(Ⅱ)证明: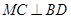 .
.
已知函数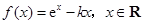 .
.
(Ⅰ)若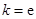 ,试确定函数
,试确定函数 的单调区间;
的单调区间;
(Ⅱ)若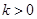 ,且对于任意
,且对于任意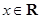 ,
,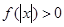 恒成立,试确定实数
恒成立,试确定实数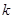 的取值范围;
的取值范围;
(Ⅲ)设函数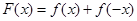 ,求证:
,求证: