如图,已知平行四边形ABCD中,BC=2,BD⊥CD,四边形ADEF为正方形,平面ADEF⊥平面ABCD.记CD=x,V(x)表示四棱锥F-ABCD的体积.
(1)求V(x)的表达式.
(2)求V(x)的最大值.
给定双曲线x2-
=1,过B(1,1)能否作直线m,使m与所给双曲线交于Q1、Q2,且B为线段Q1Q2的中点?这样的直线m如果存在,求出它的方程;如果不存在,请说明理由.
设双曲线H: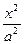 
-
=1(a>0,b>0)满足如下条件:①ab=
;②直线l过右焦点F,斜率为
,交y轴于点P,线段PF交H于Q,且|PQ|∶|QF|=2∶1.求双曲线的方程.
△ABC的三个顶点都在双曲线上,一边的两个端点是B(0,6)和C(0,-6),另两边斜率的乘积是
,求双曲线的方程.
以坐标轴为对称轴的等轴双曲线的一条准线方程为y=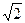
,则双曲线方程为_____________.
已知函数
.
(1)判断函数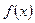
的奇偶性;
(2)判断函数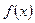在定义域内是增函数还是减函数?请说明理由;
(3)已知
,解关于
不等式: 
.