(1)计算: ;(2)解不等式组
;(2)解不等式组
已知:如图,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=2,BC=6,AB=3.E为BC边上一点,以BE为边作正方形BEFG,使正方形BEFG和梯形ABCD在BC的同侧.
(1)当正方形的顶点F恰好落在对角线AC上时,求BE的长;
(2)将(1)问中的正方形BEFG沿BC向右平移,记平移中的正方形BEFC为正方形B′EFG,当点E与点C重合时停止平移.设平移的距离为t,正方形B′EFG的边EF与AC交于点M,连接B′D,B′M,DM,是否存在这样的t,使△B′DM是直角三角形?若存在,求出t的值;若不存在,请说明理由;
(3)在(2)问的平移过程中,设正方形B′EFG与△ADC重叠部分的面积为S,请直接写出S与t之间的函数关系式以及自变量t的取值范围.
企业的污水处理有两种方式,一种是输送到污水厂进行集中处理,另一种是通过企业的自身设备进行处理.某企业去年每月的污水量均为12000吨,由于污水厂处于调试阶段,污水处理能力有限,该企业投资自建设备处理污水,两种处理方式同时进行.1至6月,该企业向污水厂输送的污水量y1(吨)与月份x(1≤x≤6,且x取整数)之间满足的函数关系如下表:
7至12月,该企业自身处理的污水量y2(吨)与月份x(7≤x≤12,且x取整数)之间满足二次函数关系式为 .其图象如图所示.1至6月,污水厂处理每吨污水的费用:
.其图象如图所示.1至6月,污水厂处理每吨污水的费用: (元)与月份x之间满足函数关系式:
(元)与月份x之间满足函数关系式: ,该企业自身处理每吨污水的费用:
,该企业自身处理每吨污水的费用: (元)与月份x之间满足函数关系式:
(元)与月份x之间满足函数关系式: ;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
;7至12月,污水厂处理每吨污水的费用均为2元,该企业自身处理每吨污水的费用均为1.5元.
(1)请观察题中的表格和图象,用所学过的一次函数、反比例函数或二次函数的有关知识,分别直接写出 与x之间的函数关系式;
与x之间的函数关系式;
(2)请你求出该企业去年哪个月用于污水处理的费用W(元)最多,并求出这个最多费用;
(3)今年以来,由于自建污水处理设备的全面运行,该企业决定扩大产能并将所有污水全部自身处理,估计扩大产能后今年每月的污水量都将在去年每月的基础上增加a%,同时每吨污水处理的费用将在去年12月份的基础上增加(a﹣30)%,为鼓励节能降耗,减轻企业负担,财政对企业处理污水的费用进行50%的补助.若该企业每月的污水处理费用为18000元,请计算出a的整数值.
(参考数据: ≈15.2,
≈15.2, ≈20.5,
≈20.5, ≈28.4)
≈28.4)
已知:如图,在菱形ABCD中,F为边BC的中点,DF与对角线AC交于点M,过M作ME⊥CD于点E,∠1=∠2.
(1)若CE=1,求BC的长;
(2)求证:AM=DF+ME.
高中招生指标到校是我市中考招生制度改革的一项重要措施.某初级中学对该校近四年指标到校保送生人数进行了统计,制成了如下两幅不完整的统计图: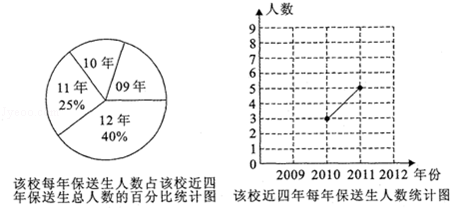
(1)该校近四年保送生人数的极差是.请将折线统计图补充完整;
(2)该校2009年指标到校保送生中只有1位女同学,学校打算从中随机选出2位同学了解他们进人高中阶段的学习情况.请用列表法或画树状图的方法,求出所选两位同学恰好是1位男同学和1位女同学的概率.