以“光盘”为主题的公益活动越来越受到社会的关注.某校为培养学生勤俭节约的习惯,随机抽查了部分学生(态度分为:赞成、无所谓、反对),并将抽查结果绘制成图1和图2(统计图不完整).请根据图中提供的信息,解答下列问题: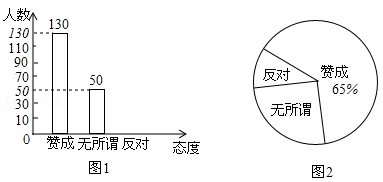
(1)此次抽样调查中,共抽查了多少名学生?
(2)将图1补充完整;
(3)根据抽样调查结果,请你估计该校3000名学生中有多少名学生持反对态度?
如图,在△ABC中,AB=AC,D、E在BC上,且AD=AE,求证:BD=CE.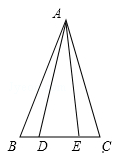
化简并求值(其中a=﹣1)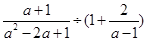
数学游戏题(本题共有2小题,第1题满分5分,第2题满分4分,共9分)
(1)下图是一个三阶幻方,有9个数字构成,并且每横行,竖行和对角线上的3个数字的和都相等,试填出空格中的数.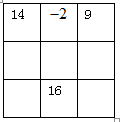
(2)有一种“二十四点”的游戏(即算24游戏),其游戏规则是这样的:任取四个1至13之间的自然数,将这四个数(每个数用且只能用一次)进行加减乘除四则运算,使其结果等于24.例如对1,2,3, 4,可作如下运算:(1+2+3)×4=24(上述运算与4×(1+2+3)视为相同方法的运算)
①给出有理数4,6,9,12;请你写出一个算式使其结果为24.
②在我们学过负数以后这个游戏仍可以玩,如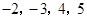 可以列出算式
可以列出算式 ;现给出
;现给出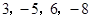 四个数,请你写出一个算式使其结果为24.
四个数,请你写出一个算式使其结果为24.
按如图所示的程序计算,若开始输入的x的值为48,我发现第一次得到的结果为24,第二次得到的结果为12,…,请你探索: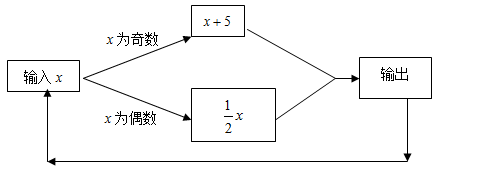
(1)第四次得到的结果;(2)第九次得到的结果;(3)第2012次得到的结果.