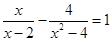如图所示，已知在直角梯形OABC中，AB∥OC，BC⊥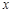
轴于点C，A
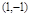，B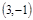
．动点P从O点出发，沿
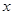轴正方向以每秒1个单位长度的速度移动．过P点作PQ垂直于直线OA，垂足为Q．设
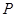点移动的时间为秒，△OPQ与直角梯形OABC重叠部分的面积为S．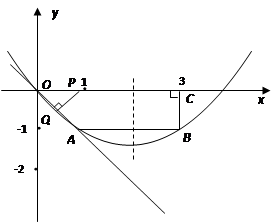
求经过O、A、B三点的抛物线解析式；
求S与t的函数关系式；
将△OPQ绕着点
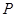逆时针旋转90°，是否存在t，使得△OPQ的顶点为O或Q在抛物线上？若存在，直接写出t的值；若不存在，请说明理由．
作图题（不写作法）
已知：如下图所示，
①作出△ABC关于y轴对称的△A1B1C1，并写出△A1B1C1三个顶点的坐标．
②在x轴上确定点P，使PA+PC最小．
某县为了落实中央的“强基惠民工程”，计划将某村的居民自来水管道进行改造．该工程若由甲队单独施工恰好在规定时间内完成；若乙队单独施工，则完成工程所需天数是规定天数的1．5倍．如果由甲、乙队先合做15天，那么余下的工程由甲队单独完成还需5天．
（1）这项工程的规定时间是多少天？
（2）已知甲队每天的施工费用为6500元，乙队每天的施工费用为3500元．为了 缩短工期以减少对居民用水的影响，工程指挥部最终决定该工程由甲、乙队合做来完成．则该工程施工费用是多少？
已知△ABC为等边三角形，点D，E分别在BC，AC边上，且AE=CD，AD与BE相交于点F．
求证：△ABE≌△CAD．
如图，CE=CB，CD=CA，∠DCA=∠ECB，求证：DE=AB．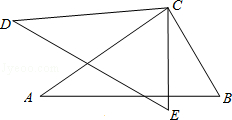
解方程：