(本题12分)如图,∠AOB为直角,∠BOC为锐角,且OM平分∠AOC,ON平分∠BOC.⑴若∠BOC=50°,试求∠MON的度数;

⑵如果⑴中的∠BOC=α(α为锐角),其
 他条件不变,试求∠MON的度数;
他条件不变,试求∠MON的度数;⑶如果⑴中∠AOB=β,其他条件不变,你能求出∠MON的度数吗?
⑷从⑴⑵⑶的结果,你能看出什么规律?

如图,矩形 中, ,将矩形 绕点 旋转得到矩形 ,使点 的对应点 落在 上, 交 于点 ,在 上取点 ,使 .
(1)求证: .
(2)求 的度数.
(3)已知 ,求 的长.

某销售商准备在南充采购一批丝绸,经调查,用10000元采购 型丝绸的件数与用8000元采购 型丝绸的件数相等,一件 型丝绸进价比一件 型丝绸进价多100元.
(1)求一件 型、 型丝绸的进价分别为多少元?
(2)若销售商购进 型、 型丝绸共50件,其中 型的件数不大于 型的件数,且不少于16件,设购进 型丝绸 件.
①求 的取值范围.
②已知 型的售价是800元 件,销售成本为 元 件; 型的售价为600元 件,销售成本为 元 件.如果 ,求销售这批丝绸的最大利润 (元 与 (元 的函数关系式(每件销售利润 售价 进价 销售成本).
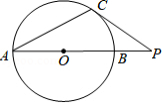
如图, 是 上一点,点 在直径 的延长线上, 的半径为3, , .
(1)求证: 是 的切线.
(2)求 的值.
如图,直线 与双曲线 交于点 , , .
(1)求直线与双曲线的解析式.
(2)点 在 轴上,如果 ,求点 的坐标.

已知关于 的一元二次方程 .
(1)求证:方程有两个不相等的实数根.
(2)如果方程的两实数根为 , ,且 ,求 的值.