下图是某传送装置的示意图。其中PQ为水平的传送带,传送带长度L=6m,与水平地面的高度为H=5m。MN是光滑的曲面,曲面与传送带相切于N点,现在有一滑块质量为m=3kg从离N点高为h=5m处静止释放,滑块与传送带间的摩擦系数为μ=0.3.重力加速度为g=10m/s2。
(1)滑块以多大的速度进入传送带?
(2)若传送带顺时针转动,请求出滑块与传送带摩擦产生的热量Q与传送带的速度v的大小关系,并作出Q与v的图象。
(3)若传送带逆时针转动,请求出物体从Q点抛出后距Q点的水平的距离与传送带的速度的关系。(认为滑块以水平速度离开传送带)
如图所示,光滑水平面上固定一辆质量M=5kg的小车,顶端用一根长L=0.45m的不可伸长细绳拴住一小球,小球的质量m=0.2kg,小球被拉到水平位置无初速度自由释放,当小球和车接触的瞬间,突然解除小车的固定并给小车一向右的速度v0=0.64m/s,小球和车碰撞过程有机械能损失,g取10m/s2,求:
i.小车最终的速度:
ii.全过程中小球损失的机械能。
如图所示是一列横渡上A、B两质点的振动图象,两质点沿波的传播方向上的距离△x=4.0m.求这列波的波速。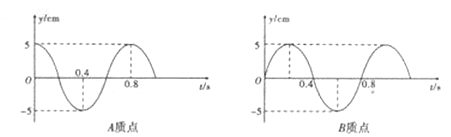
如图所示,一个横截面积S=10cm2的容器中,有一个用弹簧和底部相连的活塞,活塞质量不计,当温度为27℃时,内外压强都为p=1×105Pa,活塞和底面相距L=20cm。在活塞上放质量m=20kg的物体,活塞静止时下降10cm,温度仍为27℃,不计活塞与容器壁的摩擦,g=10m/s2。求:
i.弹簧的劲度系数k;
ii.如果把活塞内气体加热到57℃,为保持活塞静止时位置仍下降10cm,活塞上应冉加物体的质量为多少。
如图甲所示,已知足够长的传送带与水平面成θ=15°角,质量m=1kg的小物体以v0=2m/s的速度由P沿传送带滑人,物体滑人瞬间,传送带以加速度a无初速度逆时针加速转动,a—t图象如图乙所示,物体与传送带间的动摩擦因数u="0" 1,试分析5秒内小物体加速度的大小并求5秒内小物体相对于传送带的位移大小。(g=10m/s2.sin15°=0.26.cos15°=0.96)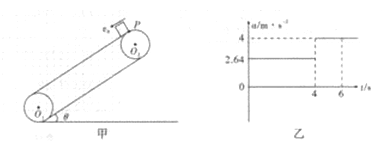
如图所示,小球从A点以固定的初速度v0水平抛出,空气阻力不计,A点右下方有一带挡板的轮子,轮子与小球运动轨迹在同一竖直面内。轮子的半径为R,抛出点A比轮轴高h,挡板的初位置在与轮轴等高的B点,调整轮轴O的位置,使平抛轨迹与轮缘相切于C,OC与OB间夹角为θ角。求: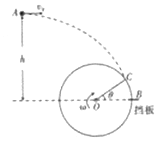
(l)小球抛出的初速度v0大小为多少;
(2)小球抛出的瞬间轮子开始顺时针匀速转动,若不计挡板大小,要使小球打在挡板上,轮子转动的角速度为多少?