如图,函数f(x)=x+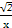 的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.
的定义域为(0,+∞).设点P是函数图象上任一点,过点P分别作直线y=x和y轴的垂线,垂足分别为M,N.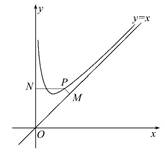
(1)证明:|PM|·|PN|为定值.
(2)O为坐标原点,求四边形OMPN面积的最小值.
(本小题满分10分)
已知函数 .
.
(1)求函数 的定义域;(2)判断
的定义域;(2)判断 的奇偶性;
的奇偶性;
(3)方程 是否有根?如果有根
是否有根?如果有根 ,请求出一个长度为
,请求出一个长度为 的区间
的区间 ,使
,使 ;如果没有,请说明理由?(注:区间
;如果没有,请说明理由?(注:区间 的长度
的长度 ).
).
(本小题12分)已知二次函数 满足
满足 且
且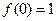 .
.
(1)求 的解析式;
的解析式;
(2) 当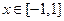 时,不等式:
时,不等式: 恒成立,求实数
恒成立,求实数 的范围.
的范围.
(3)设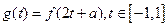
 ,求
,求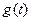 的最大值;
的最大值;
(本小题10分)已知函数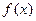 =
=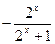 .
.
(1)用定义证明函数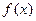 在(-∞,+∞)上为减函数;
在(-∞,+∞)上为减函数;
(2)若x [1,2],求函数
[1,2],求函数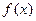 的值域;
的值域;
(3)若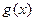 =
= ,且当
,且当 x
x [1,2]时
[1,2]时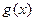
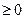 恒成立,求实数
恒成立,求实数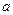 的取值范围.
的取值范围.
(本小题8分)经过调查发现,某种新产品在投 放市场的30天中,前20天其价格直线上升,后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示:
放市场的30天中,前20天其价格直线上升,后10天价格呈直线下降趋势。现抽取其中4天的价格如下表所示:
| 时间 |
第4天 |
第12天 |
第20天 |
第28天 |
| 价格 (千元) |
34 |
42 |
50 |
34 |
(1)写出价格 关于时间
关于时间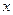 的函数表达式(
的函数表达式(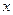 表示投放市场的第
表示投放市场的第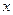 天)
天)
(2)若销售量 与时间
与时间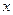 的函数关系式为
的函数关系式为 :
: ,问该产品投放市场第几天,日销售额最高?
,问该产品投放市场第几天,日销售额最高?
(本题8分)全集U=R,若集合 ,
,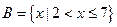 ,
,
则(结果用区间表示)
(1)求 ; (
; ( 2)若集合C=
2)若集合C= ,
,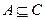 ,求
,求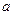 的取值范围;
的取值范围;