下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.
| x |
3 |
4 |
5 |
6 |
| y |
2.5 |
3 |
4 |
4.5 |
(1)请画出上表数据的散点图.
(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程 =bx+a.
=bx+a.
(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)
为选拔选手参加“中国谜语大会”,某中学举行了一次“谜语大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为 分)作为样本(样本容量为
分)作为样本(样本容量为 )进行统计.按照
)进行统计.按照 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在 的数据).
的数据).
(1)求样本容量 和频率分布直方图中的
和频率分布直方图中的 、
、 的值;
的值;
(2)在选取的样本中,从竞赛成绩在 分以上(含
分以上(含 分)的学生中随机抽取
分)的学生中随机抽取 名学生参加“中国谜语大会”,求所抽取的
名学生参加“中国谜语大会”,求所抽取的 名学生中至少有一人得分在
名学生中至少有一人得分在 内的概率.
内的概率.
改革开放以来,我国高等教育事业有了突飞猛进的发展,有人记录了某村 到
到 年五年间每年考入大学的人数,为了方便计算,
年五年间每年考入大学的人数,为了方便计算, 年编号为
年编号为 ,
,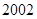 年编号为
年编号为 ,……,
,……, 年编号为
年编号为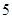 ,数据如下:
,数据如下:
根据这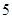 年的数据,利用最小二乘法求出
年的数据,利用最小二乘法求出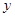 关于
关于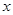 的回归方程
的回归方程 ,并计算第
,并计算第 年的估计值.
年的估计值.
参考:用最小二乘法求线性回归方程系数公式
已知两个关于x的一元二次方程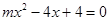 和
和 ,求两方程的根都是整数的充要条件.
,求两方程的根都是整数的充要条件.
已知 ,
,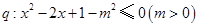 ,若
,若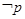 是
是 的必要而不充分条件,求实数
的必要而不充分条件,求实数 的取值范围.
的取值范围.
已知函数 ,
, .
.
(1)若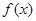 在
在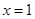 处与直线
处与直线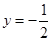 相切,求a,b的值;
相切,求a,b的值;
(2)在(1)的条件下,求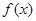 在
在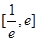 上的最大值;
上的最大值;
(3)若不等式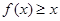 对所有的
对所有的 ,
, 都成立,求a的取值范围.
都成立,求a的取值范围.