探究函数f(x)=x+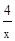 ,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
,x∈(0,+∞)的最小值,并确定取得最小值时x的值.列表如下:
| x |
… |
0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
| y |
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.02 |
4.04 |
4.3 |
5 |
5.8 |
7.57 |
… |
请观察表中y值随x值变化的特点,完成以下的问题.
函数f(x)=x+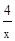 (x>0)在区间(0,2)上递减;
(x>0)在区间(0,2)上递减;
(1)函数f(x)=x+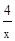 (x>0)在区间上递增.
(x>0)在区间上递增.
当x=时,y最小=.
(2)证明:函数f(x)=x+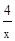 在区间(0,2)上递减.
在区间(0,2)上递减.
(3)思考:函数f(x)=x+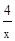 (x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
(x<0)有最值吗?如果有,那么它是最大值还是最小值?此时x为何值?(直接回答结果,不需证明)
已知函数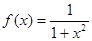
(1)判断 的奇偶性;
的奇偶性;
(2)确定函数 在
在 上是增函数还是减函数?证明你的结论.
上是增函数还是减函数?证明你的结论.
已知
(1)求当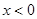 时,函数
时,函数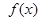 的表达式;
的表达式;
(2)作出函数 的图象,并指出其单调区间。
的图象,并指出其单调区间。
设定义在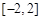 上的奇函数f(x)在
上的奇函数f(x)在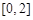 上是减函数,若f(1-m)< f(m)
上是减函数,若f(1-m)< f(m)
求 的取值范围.
的取值范围.
市内电话费是这样规定的,每打一次电话不超过3分钟付电话费0.18元,超过3分钟而不超过6分钟的付电话费0.36元,依次类推,每次打电话
 分钟应付话费y元,写出函数解析式并画出函数图象.
分钟应付话费y元,写出函数解析式并画出函数图象.