从原点O引直线交直线2x+4y-1=0于点M,P为OM上一点,已知OP·OM=1,求P点所在曲线的极坐标方程.
(本小题满分12分)
某客运公司争取到一个相距100海里的甲、乙两地的客运航线权。已知轮船的平均载客人数为200人,轮船每小时使用的燃料费和轮船航行速度的平方成正比,轮船的最大速度为20海里/小时,当船速为10海里/小时,它的燃料费用是每小时60元,其余费用(不论速度如何)总计是每小时150元,假定轮船从甲地到乙地匀速航行。
(I)求轮船每小时的燃料费W与速度v的关系式;
(II)若公司打算从每位乘客身上获得利润10元,那么该公司设计的船票价格最低可以是多少?(精确到1元,参考数据: )
)
(本小题满分12分)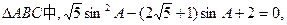 A是锐角。
A是锐角。
(I)求 的值;
的值;
(II)若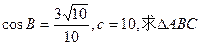 的面积。
的面积。
(本小题满分12分)已知△ABC三个内角A、B、C的对边分别为a、b、c,向量 。
。
(1)求A;
(2)已知 ,求bc的最大值。
,求bc的最大值。
(本小题满分12分)将一张2×6米的硬钢板按图纸的要求进行操作:沿线裁去阴影部分,把剩余的部分按要求焊接成一个有盖的长方体水箱(⑦为底,①②③④为侧面,⑤+⑥为水箱盖,其中①与③、②与④分别是全等的矩形,且⑤+⑥=⑦),设水箱的高为x米,容积为y立方米。
(1)写出y关于x的函数关系式;
(2)如何设计x的大小,使得水箱的容积最大?
(本小题满分12分)设函数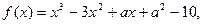 若它是R上的单调函数,且1是它的零点。
若它是R上的单调函数,且1是它的零点。
(1)求实数a的值;
|
(2)设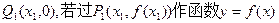 的图象的切线与x轴交于点
的图象的切线与x轴交于点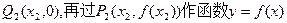 的图象的切线与x轴于
的图象的切线与x轴于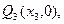 ……,依此下去,过
……,依此下去,过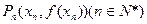 作函数
作函数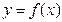 的图象的切线与x轴交于点
的图象的切线与x轴交于点 ……,若
……,若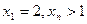 求证:
求证: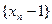 成等比数列;并求数列
成等比数列;并求数列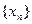 的通项公式
的通项公式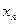 。(已知
。(已知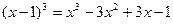 )
)