设函数f(x)=xn+bx+c(n∈N+,b,c∈R).
(1)设n≥2,b=1,c=-1,证明:f(x)在区间(
,1)内存在唯一零点;
(2)设n为偶数,|f(-1)|≤1,|f(1)|≤1,求b+3c的最小值和最大值;
(3)设n=2,若对任意x1,x2∈[-1,1],有|f(x1)-f(x2)|≤4,求b的取值范围.
已知函数f（x）是定义在R上的增函数．
（1）a
R，试比较f（a2）与f（a-1）的大小，并说明理由；
（2）若对任意的xR，不等式f（ax2）﹤f（ax+1）恒成立．求实数a的取值范围．
已知函数f（x）＝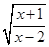
的定义域为集合A，函数g（x）＝
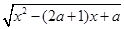的定义域为集合B．
（1）求集合A，B；
（2）若A∩B＝A，求实数a的取值范围．
已知函数f（x）＝
（1）求f（1）+f（2）+f（3）+f（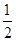
）+f（
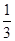）的值；
（2）求f（x）的值域．
设集合A＝{x|x2-x+m＝0}，B＝{x|x2+px+q＝0}，且A∩B＝{1}，A∪B＝A．
（1）求实数m的值；
（2）求实数p，q的值．
设二次函数f（x）=ax2+bx+c（a＞0），方程f（x）﹣x=0的两个根x1，x2满足：0＜x1＜x2＜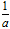
．
（1）当x∈（0， x1）时，证明x＜f（x）＜x1；
（2）设函数f（x）的图象关于直线x=x0对称，证明x0＜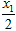
．