(16分)已知函数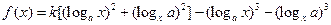 , (其中
, (其中 ),
), ,设
,设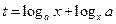 .
.
(Ⅰ)当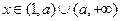 时,试将
时,试将 表示成
表示成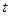 的函数
的函数 ,并探究函数
,并探究函数 是否有极值;
是否有极值;
(Ⅱ)当k=4时,若对任意的 ,存在
,存在 ,使
,使 ,试求实数b的取值范围.。
,试求实数b的取值范围.。
(满分12分)已知点F为抛物线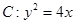 的焦点,点P时准线
的焦点,点P时准线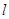 上的动点,直线PF交抛物线C于A、B两点,若点P的纵坐标为
上的动点,直线PF交抛物线C于A、B两点,若点P的纵坐标为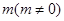 ,点D为准线
,点D为准线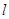 与
与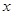 轴的交点。
轴的交点。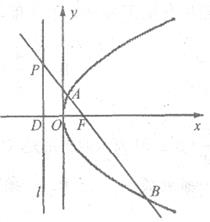
(Ⅰ)求直线PF的方程;
(Ⅱ)求△DAB的面积S的范围;
(Ⅲ)设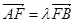 ,
,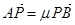 ,求证
,求证 为定值。
为定值。
(满分12分)甲、乙、丙三人独立破译同一份密码,已知甲、乙、丙各自破译出密码的概率分别为 。且他们是否破译出密码互不影响。若三人中只有甲破译出密码的概率为
。且他们是否破译出密码互不影响。若三人中只有甲破译出密码的概率为 。
。
(Ⅰ)求 的值;
的值;
(Ⅱ)设甲、乙、丙三人中破译出密码的人数为X,求X得分布列和数学期望EX。
(满分12分)如图,在直三棱柱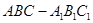 中,∠ACB=90°;AC=BC=CC1=2。
中,∠ACB=90°;AC=BC=CC1=2。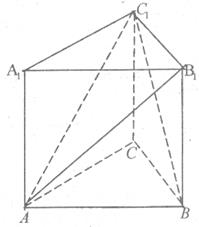
(1)求证:AB1⊥BC1;
(2)求点B到平面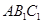 的距离;
的距离;
(3)求二面角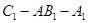 的大小。
的大小。
(满分12分)在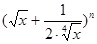 的展开式中,前三项的系数成等差数列。
的展开式中,前三项的系数成等差数列。
(Ⅰ)求展开式中含有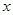 的项的系数;
的项的系数;
(Ⅱ)求展开式中的有理项。
(满分10分)在曲线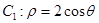 上求一点,使它到直线
上求一点,使它到直线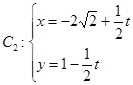 (
(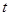 为参数)的距离最小,并求出该点坐标和最小距离。
为参数)的距离最小,并求出该点坐标和最小距离。