请你设计一个包装盒，如图所示，ABCD是边长为60 cm的正方形硬纸片，切去阴影部分所示的四个全等的等腰直角三角形，再沿虚线折起，使得A，B，C，D四个点重合于图中的点P，正好形成一个正四棱柱形状的包装盒，E，F在AB上，是被切去的一个等腰直角三角形，斜边的两个端点，设AE＝FB＝x(cm)．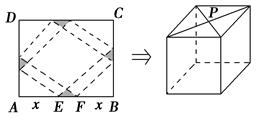
①某广告商要求包装盒的侧面积S(cm2)最大，试问x应取何值？
②某厂商要求包装盒的容积V(cm3)最大，试问x应取何值？并求出此时包装盒的高与底面边长的比值．
(本小题满分12分）
已知
求证：
三、解答题（本大题共6小题,共70分．解答应写出文字说明,证明过程或演算步骤．）
17. (本小题满分10分）
已知复数
,若
,
⑴求
;
⑵求实数
的值
如图，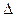
ABC和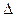DBC所在的平面互相垂直，且AB=BC=BD，
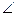CBA=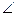DBC= 60°，(1) 求证：直线AD⊥直线BC；(2)求直线AD与平面BCD所成角的大小。
某高速公路某施工工地需调运建材100吨，可租用装载的卡车和农用车分别为10辆和20辆，若每辆卡车装载8吨，运费960元，每辆农用车装载2.5吨，运费360元，问两种车各租用多少辆时，才能一次性装完且总费用最低？
如图为函数y=Asin(ωx+φ)(A＞0,ω＞0)的图象的一部分，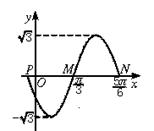
试求该函数的一个解析式.