复数z= 且|z|=4,z对应的点在第一象限,若复数0,z,
且|z|=4,z对应的点在第一象限,若复数0,z, 对应的点是正三角形的三个顶点,求实数a、b的值.
对应的点是正三角形的三个顶点,求实数a、b的值.
(本小题满分12分)
如图,直三棱柱A1B1C1—ABC中,C1C=CB=CA=2,AC⊥CB.
D、E分别为棱C1C、B1C1的中点.
(1)求二面角B—A1D—A的平面角余弦值;
(2)在线段AC上是否存在一点F,使得EF⊥平面A1BD?
若存在,确定其位置并证明结论;若不存在,说明理由.
(本小题满分13分) 设椭圆
设椭圆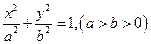 的左右焦点分别为
的左右焦点分别为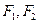 ,离心率
,离心率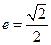 ,过
,过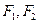 分别作直线
分别作直线 ,且
,且 ,
, 分别交直线
分别交直线 :
: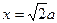 于
于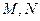 两点。
两点。
(Ⅰ)若 ,求 椭圆的方程;
,求 椭圆的方程;
(Ⅱ)当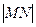 取最小值时,试探究
取最小值时,试探究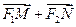 与
与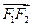
的关系,并证明之.
(本小题满分12分)函数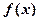 是一次函数,且
是一次函数,且 ,
, ,其中
,其中 自然对数的底。(1)求函数
自然对数的底。(1)求函数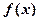 的解析式, (2)在数列
的解析式, (2)在数列 中,
中,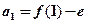 ,
, ,求数列
,求数列 的通项公式;(3若数列
的通项公式;(3若数列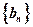 满足
满足 ,试求数列
,试求数列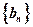 的前
的前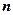 项和
项和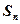 。
。
(本小题满分12分)某市十所重点中学进行高三联考,共有5000名考生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表: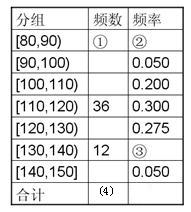
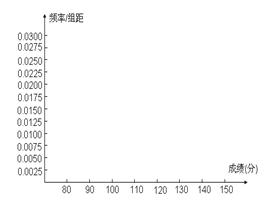
(1)根据上面频率分布表,求①,②,③,④处的数值
(2)在所给的坐标系中画出区间[80,150]上的频率分布直方图;
(3)从整体中任意抽取3个个体,成绩落在[105,120]中的个体数目为ξ ,求ξ的分布列和数学期望.
(本小题满分12分)已知两个向量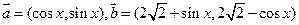 ,
,
f(x)= 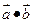 ,
, (1)求f(x)的值域;(2)若
(1)求f(x)的值域;(2)若 ,求
,求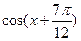 的值
的值