一次函数y=ax+b（a≠0）、二次函数y=ax2+bx和反比例函数y=
（k≠0）在同一直角坐标系中的图象如图所示，A点的坐标为（-2，0），则下列结论中，正确的是（ ）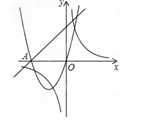
| A．b=2a+k | B．a=b+k | C．a＞b＞0 | D．a＞k＞0 |
满足下列条件的各对三角形中相似的两个三角形有（）．
| A．∠A=60°，AB=5cm，AC=10cm；∠A′=60°，A′B′=3cm，A′C′=10cm |
| B．∠A=45°，AB=4cm，BC=6cm；∠D=45°，DE=2cm，DF=3cm |
| C．∠C=∠E=30°，AB=8cm，BC=4cm；DF=6cm，FE=3cm |
| D．∠A=∠A′，且AB·A′B′=AC·A′B′ |
如图，已知△ABC，D，E分别是AB，AC边上的点．AD=3cm，AB=8cm，AC=10cm．若△ADE∽△ABC，则AE的值为（）．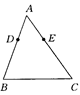
A． |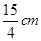
B． |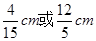
C． |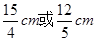
D． |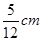
下列图形不一定相似的是（）．
| A．有一个角是120°的两个等腰三角形; |
| B．有一个角是60°的两个等腰三角形 |
| C．两个等腰直角三角形; |
| D．有一个角是45°的两个等腰三角形 |
如图所示的测量旗杆的方法，已知AB是标杆，BC表示AB在太阳光下的影子，叙述错误的是（）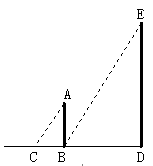
| A．可以利用在同一时刻，不同物体与其影长的比相等来计算旗杆的高 |
| B．只需测量出标杆和旗杆的影长就可计算出旗杆的高 |
| C．可以利用△ABC∽△EDB，来计算旗杆的高 |
| D．需要测量出AB、BC和DB的长，才能计算出旗杆的高 |
如图，能使△ACD∽△BCA全等的条件是（）
A． |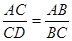
B． |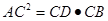
C． |
D． |