设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x),当x∈[0,2]时,f(x)=2x-x2.
(1)求证:f(x)是周期函数;
(2)当x∈[2,4]时,求f(x)的解析式;
(3)计算f(0)+f(1)+f(2)+…+f(2014)的值.
选修4-5:不等式选讲
已知函数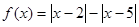 .
.
(1)证明: ;
;
(2)求不等式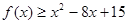 的解集.
的解集.
选修4-4:坐标系与参数方程选讲
在直角坐标系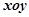 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( 为参数),以原点为极点,以
为参数),以原点为极点,以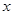 轴正半轴为极轴,建立极坐标系,曲线
轴正半轴为极轴,建立极坐标系,曲线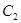 的极坐标方程为
的极坐标方程为 .
.
(1)求曲线 的普通方程与曲线
的普通方程与曲线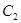 的直角坐标方程;
的直角坐标方程;
(2)设点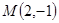 ,曲线
,曲线 与曲线
与曲线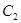 交于
交于 ,求
,求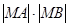 的值.
的值.
选修4-1:几何证明选讲.
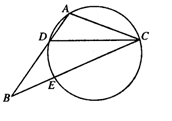
如图,在 中,
中, 是
是 的角平分线,
的角平分线,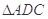 的外接圆交
的外接圆交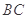 于点
于点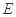 ,
,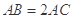 .
.
(Ⅰ)求证: ;
;
(Ⅱ)当 时,求
时,求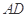 的长.
的长.
已知函数 R).
R).
(1)若曲线 在点
在点 处的切线与直线
处的切线与直线 平行,求
平行,求 的值;
的值;
(2)在(1)条件下,求函数 的单调区间和极值;
的单调区间和极值;
(3)当 ,且
,且 时,证明:
时,证明:
已知椭圆 的左顶点为
的左顶点为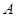 ,
, 是椭圆
是椭圆 上异于点
上异于点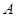 的任意一点,点
的任意一点,点 与点
与点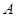 关于点
关于点 对称.
对称.
(1)若点 的坐标为
的坐标为 ,求
,求 的值;
的值;
(2)若椭圆 上存在点
上存在点 ,使得
,使得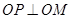 ,求
,求 的取值范围.
的取值范围.