经市场调查，某种商品在过去50天的销量和价格均为销售时间t(天)的函数，且销售量近似地满足f(t)＝－2t＋200(1≤t≤50，t∈N)，前30天价格为g(t)＝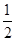
t＋30(1≤t≤30，t∈N)，后20天价格为g(t)＝45(31≤t≤50，t∈N)．
(1)写出该种商品的日销售额S与时间t的函数关系式；
(2)求日销售额S的最大值．
已知命题
：“椭圆
的焦点在x轴上”
命题
在
上单调递增，若
为假，求
的取值范围．
.已知函数
.
（Ⅰ）求证: 对于任意的
(
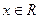)都有
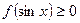恒成立
（Ⅱ）若锐角
满足
,求
.
(Ⅲ)若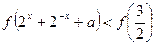
对于任意的
恒成立,求
的取值范围.
.已知函数
在一个周期内的部分函数图象如图所示.
（Ⅰ）求函数
的解析式.
（Ⅱ）求函数的单调递增区间.
(Ⅲ)求函数在区间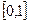
上的最大值和最小值.
若函数
.
（Ⅰ）求函数
的定义域,判断函数的奇偶性.
（Ⅱ）若关于
（
）的方程
,求.
甲盒中有1个黑球1个白球;乙盒中有1个黑球2个红球．这些
球除了颜色不同外其余无差别.
（Ⅰ）从两个盒子中各取1个球,求取出的两个球颜色不同的概率.
（Ⅱ）若把两盒中所有的球混合后放入丙盒中.从丙盒中一次取出两个球，求取出的两个球颜色不同的概率
．