如图,ABCD是正方形空地,边长为30m,电源在点P处,点P到边AD、AB距离分别为9m、3m.某广告公司计划在此空地上竖一块长方形液晶广告屏幕MNEF,MN∶NE=16∶9.线段MN必须过点P,端点M、N分别在边AD、AB上,设AN=x(m),液晶广告屏幕MNEF的面积为S(m2).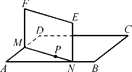
(1)用x的代数式表示AM;
(2)求S关于x的函数关系式及该函数的定义域;
(3)当x取何值时,液晶广告屏幕MNEF的面积S最小?
附加题(按满分5分计入总分,若总分超过满分值以满分计算)
如果集合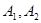 满足
满足 ,则称(
,则称(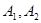 )为集合
)为集合 的一种分拆.并规定:当且仅当
的一种分拆.并规定:当且仅当 时,(
时,(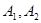 )与(
)与(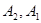 )为集合
)为集合 的同一种分拆.请计算集合
的同一种分拆.请计算集合 所有不同的分拆种数有多少种?
所有不同的分拆种数有多少种?
已知函数 满足:①定义在
满足:①定义在 上;②当
上;②当 时,
时,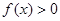 ;③对于任意的
;③对于任意的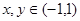 ,有
,有 .
.
(1)取一个对数函数 ,验证它是否满足条件②,③;
,验证它是否满足条件②,③;
(2)对于满足条件①,②,③的一般函数 ,判断
,判断 是否具有奇偶性和单调性,并加以证明.
是否具有奇偶性和单调性,并加以证明.
已知函数 (
( )
)
(1)若 ,作出函数
,作出函数 的图象;
的图象;
(2)设 在区间
在区间 上的最小值为
上的最小值为 ,求
,求 的表达式.
的表达式.
如图是一块形状为直角三角形的铁皮,两条直角边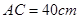 ,
, .
.
现在要将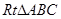 剪成一个矩形
剪成一个矩形 ,设
,设 ,
,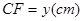 .
.
(1)试用 表示
表示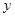 ;
;
(2)问如何截取矩形 ,才能使剩下
,才能使剩下
的残料最少?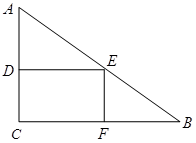
已知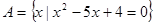 ,
,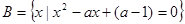 ,
, ,若
,若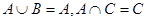 ,求实数
,求实数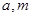 的值.
的值.