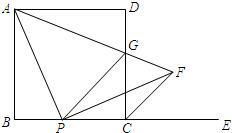
如图,在正方形 中,
中,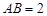 ,点
,点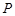 是边
是边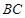 上的任意一点,
上的任意一点,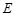 是
是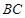 延长线上一点,联结
延长线上一点,联结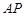 ,作
,作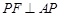 交
交 的平分线
的平分线 上一点
上一点 ,联结
,联结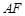 交边
交边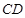 于点
于点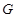 .
.
(1)求证: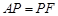 ;
;
(2)设点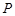 到点
到点 的距离为
的距离为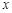 ,线段
,线段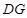 的长为
的长为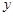 ,试求
,试求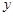 关于
关于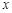 的函数关系式,并写出自变量
的函数关系式,并写出自变量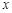 的取值范围;
的取值范围;
(3)当点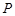 是线段
是线段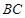 延长线上一动点,那么(2)式中
延长线上一动点,那么(2)式中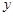 与
与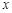 的函数关系式保持不变吗?如改变,试直接写出函数关系式.
的函数关系式保持不变吗?如改变,试直接写出函数关系式.
⑴解不等式组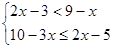
⑵解方程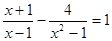
阅读理解:对于任意正实数a、b,∵( -
- )2≥0,∴a-2
)2≥0,∴a-2 +b≥0,∴a+b≥2
+b≥0,∴a+b≥2 ,只有当a=b时,等号成立.
,只有当a=b时,等号成立.
结论:在a+b≥2 (a、b均为正实数)中,若ab为定值p,则a+b≥2
(a、b均为正实数)中,若ab为定值p,则a+b≥2 ,只有当a=b时,a+b有最小值2
,只有当a=b时,a+b有最小值2 .根据上述内容,回答下列问题:
.根据上述内容,回答下列问题:
(1)若m>0,只有当m=时,m+ 有最小值;
有最小值;
若m>0,只有当m=时,2m+ 有最小值.
有最小值.
(2)如图,已知直线L1:y= x+1与x轴交于点A,过点A的另一直线L2与双曲线y=
x+1与x轴交于点A,过点A的另一直线L2与双曲线y=
(x>0)相交于点B(2,m),求直线L2的解析式.
(3)在(2)的条件下,若点C为双曲线上任意一点,作CD∥y轴交直线L1于点D,试
求当线段CD最短时,点A、B、C、D围成的四边形面积.
如图,已知反比例函数y=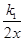 的图象与一次函数y=k2x+b的图象交于A,
的图象与一次函数y=k2x+b的图象交于A,
B两点,A(1,n),B(-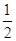 ,-2).
,-2).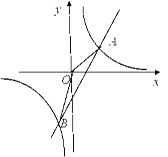
(1)求反比例函数和一次函数的解析式;
(2)当x为何值时,一次函数的值大于反比例函数的值?
(3)求△AOB的面积.
据报道,清明节期间,江阴消防大队出警多次.其中有一次是发生火灾的地方离江阴消防大队有15千米,消防大队接到报警后马上出发,先经过市区3千米,然后直接驶向火灾发生地,共用了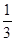 小时,已知消防车驶出市区后的速度是它在市区速度的2倍,求消防车在市区行驶的速度.
小时,已知消防车驶出市区后的速度是它在市区速度的2倍,求消防车在市区行驶的速度.
已知:如下图,△ABC是等边三角形,D为AC上任一点,∠ABD=∠ACE,BD=CE.
求证:△ADE是等边三角形.