在某次体检中,有6位同学的平均体重为65公斤.用 表示编号为
表示编号为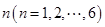 的同学的体重,且前5位同学的体重如下:
的同学的体重,且前5位同学的体重如下:
| 编号n |
1 |
2 |
3 |
4 |
5 |
| 体重xn |
60 |
66 |
62 |
60 |
62 |
(1)求第6位同学的体重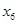 及这6位同学体重的标准差
及这6位同学体重的标准差 ;
;
(2)从前5位同学中随机地选2位同学,求恰有1位同学的体重在区间 中的概率.
中的概率.
菱形 的边长为3,
的边长为3, 与
与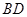 交于
交于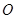 ,且
,且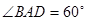 .将菱形
.将菱形 沿对角线
沿对角线 折起得到三棱锥
折起得到三棱锥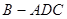 (如图),点
(如图),点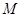 是棱
是棱 的中点,
的中点, .
.
(1)求证:平面
 平面
平面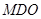 ;
;
(2)求三棱锥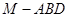 的体积.
的体积.
已知 ,不等式
,不等式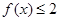 的解集为
的解集为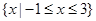 .
.
(1)求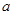 的值;
的值;
(2)若 对一切实数
对一切实数 恒成立,求实数
恒成立,求实数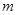 的取值范围.
的取值范围.
已知
(1)若 ,求
,求 的极大值点;
的极大值点;
(2)若 且
且 存在单调递减区间,求
存在单调递减区间,求 的取值范围.
的取值范围.
已知椭圆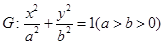 过点
过点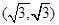 ,且离心率为
,且离心率为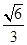 .斜率为
.斜率为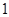 的直线
的直线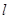 与椭圆
与椭圆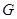 交于A、B两点,以
交于A、B两点,以 为底边作等腰三角形,顶点为
为底边作等腰三角形,顶点为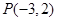 .
.
(1)求椭圆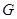 的方程;
的方程;
(2)求△ 的面积.
的面积.