如图,动物园要围成相同面积的长方形虎笼四间.一面可利用原有的墙,其他各面用钢筋网围成.
(1)现有可围成36m长的材料,每间虎笼的长、宽各设计为多少时,可使每间虎笼的面积最大?
(2)若使每间虎笼的面积为24m2,则每间虎笼的长、宽各设计为多少时,可使围成的四间虎笼的钢筋网总长最小?
(本小题满分13分) 已知集合 ,
,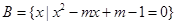 .若
.若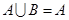 ,求实数
,求实数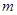 的取值范围.
的取值范围.
(本小题满分14分) 在平面直角坐标系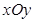 中,已知圆
中,已知圆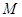 过坐标原点O且圆心在曲线
过坐标原点O且圆心在曲线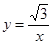 上.
上.
(1)若圆M分别与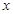 轴、
轴、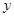 轴交于点
轴交于点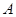 、
、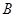 (不同于原点O),求证:
(不同于原点O),求证: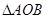 的面积为定值;
的面积为定值;
(2)设直线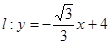 与圆M 交于不同的两点C,D,且
与圆M 交于不同的两点C,D,且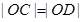 ,求圆M的方程;
,求圆M的方程;
(3)设直线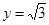 与(2)中所求圆M交于点
与(2)中所求圆M交于点 、
、 ,
, 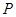 为直线
为直线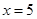 上的动点,直线
上的动点,直线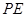 ,
,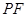 与圆M的另一个交点分别为
与圆M的另一个交点分别为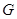 ,
, ,求证:直线
,求证:直线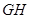 过定点.
过定点.
(本小题满分13分)设函数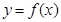 的定义域为
的定义域为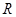 ,并且满足
,并且满足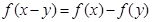 ,且
,且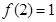 ,当
,当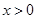 时,
时,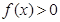
(1)求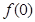 的值;
的值;
(2)判断函数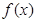 的奇偶性;
的奇偶性;
(3)如果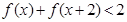 ,求
,求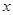 的取值范围.
的取值范围.
(本小题满分12分)如图,四棱锥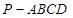 的底面是正方形,
的底面是正方形,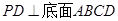 ,点
,点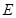 在棱
在棱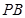 上.
上.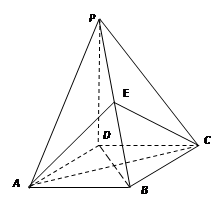
(1)求证:平面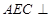 平面
平面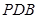 ;
;
(2)当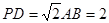 ,且
,且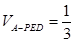 时,确定点
时,确定点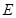 的位置,即求出
的位置,即求出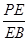 的值.
的值.
(本小题满分12分)已知圆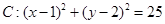 ,直线
,直线 ,
,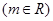 。
。
(1)证明:不论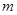 取什么实数,直线
取什么实数,直线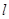 与圆恒交于两点;
与圆恒交于两点;
(2)求直线被圆 截得的弦长最小时
截得的弦长最小时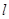 的方程.
的方程.