设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入5个盒子内. (答题要求:先列式,后计算)
(1)恰有一个盒子空着,共有多少种投放方法?
(2)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
已知函数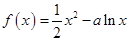 (
( )
)
(1)若函数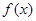 的图象在
的图象在 处的切线方程为
处的切线方程为 ,求
,求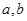 的值;
的值;
(2)若函数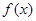 在
在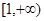 为增函数,求
为增函数,求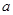 的取值范围.
的取值范围.
已知抛物线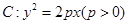 上横坐标为
上横坐标为 的点
的点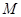 到焦点
到焦点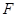 的距离为
的距离为 .
.
(1)求抛物线的方程;
(2)若斜率为 的直线
的直线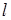 与抛物线
与抛物线 交于
交于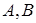 两点,且点
两点,且点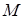 在直线
在直线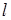 的右上方,求证:△
的右上方,求证:△ 的内心在直线
的内心在直线 上.
上.
如图,侧棱垂直底面的三棱柱 中,
中,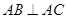 ,
, ,
,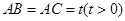 ,
,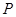 是侧棱
是侧棱 上的动点.
上的动点.
(1)当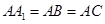 时,求证:
时,求证: ;
;
(2)若二面角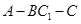 的平面角的余弦值为
的平面角的余弦值为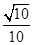 ,试求实数
,试求实数 的值.
的值.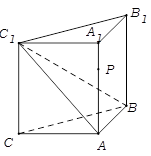
已知两个集合 ,
,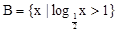 ;命题p:实数m为小于6的正实数,命题q:A是B成立的必要不充分条件,若命题
;命题p:实数m为小于6的正实数,命题q:A是B成立的必要不充分条件,若命题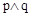 是真命题,求实数m的值.
是真命题,求实数m的值.