已知数列{an}前n项和为Sn,且a2an=S2+Sn对一切正整数都成立.
(1)求a1,a2的值;
(2)设a1>0,数列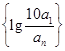 前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
前n项和为Tn,当n为何值时,Tn最大?并求出最大值.
如图,正四棱锥 中,
中,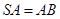 ,
,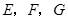 分别为
分别为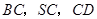 的中点,设
的中点,设 为线段
为线段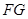 上任意一点。
上任意一点。
(Ⅰ)求证: ;
;
(Ⅱ)当直线 与平面
与平面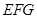 所成的角取得最大值时,求二面角
所成的角取得最大值时,求二面角 的平面角的余弦值.
的平面角的余弦值.
在 中,内角
中,内角 所对的边长分别为
所对的边长分别为 ,
,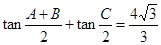 .
.
(Ⅰ)求角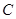 的大小;
的大小;
(Ⅱ)已知 不是钝角三角形,且
不是钝角三角形,且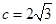 ,
, 求
求 的面积.
的面积.
(本小题满分14分)已知 为实数,对于实数
为实数,对于实数 和
和 ,定义运算“
,定义运算“ ”:
”: ,
,
设 .
.
(Ⅰ)若 在
在 上为增函数,求实数
上为增函数,求实数 的取值范围;
的取值范围;
(Ⅱ)若方程 有三个不同的解,记此三个解的积为
有三个不同的解,记此三个解的积为 ,求
,求 的取值范围.
的取值范围.
(本小题满分15分)如图,设抛物线 的焦点为
的焦点为 ,
, 为抛物线的顶点.过
为抛物线的顶点.过 作抛物线
作抛物线
的弦 ,直线
,直线 ,
, 分别交直线
分别交直线 于点
于点 ,
, .
.
(Ⅰ)当 时,求
时,求 的值;
的值;
(Ⅱ)设直线 的方程为
的方程为 ,记
,记 的面积为
的面积为 ,求
,求 关于
关于 的解析式.
的解析式.
(本小题满分15分)如图,已知 平面
平面 ,
, ,
, ,
, ,
,
为等边三角形.
(Ⅰ)求证:平面 平面
平面 ;
;
(Ⅱ)求 与平面
与平面 所成角的正弦值.
所成角的正弦值.