已知数列{an}满足a1+a2+…+an=n2(n∈N*).
(1)求数列{an}的通项公式;
(2)对任意给定的k∈N*,是否存在p,r∈N*(k<p<r)使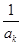 ,
,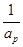 ,
,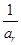 成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.
成等差数列?若存在,用k分别表示p和r(只要写出一组);若不存在,请说明理由.
已知函数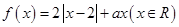 有最小值.
有最小值.
(Ⅰ)求实数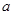 的取值范围;
的取值范围;
(Ⅱ)设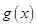 为定义在
为定义在 上的奇函数,且
上的奇函数,且 时,
时, ,求
,求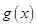 的解析式.
的解析式.
在四棱锥 中,底面
中,底面 是边长为
是边长为 的菱形,
的菱形, ,
, 面
面 ,
, ,
, ,
, 分别为
分别为 ,
, 的中点.
的中点.
(Ⅰ)求证: 面
面 ;
;
(Ⅱ)求点 到面
到面 的距离.
的距离.
若函数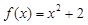 ,
, 的定义域都是集合
的定义域都是集合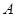 ,函数
,函数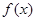 和
和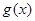 的值域分别为
的值域分别为 和
和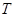 .
.
(Ⅰ)若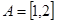 ,求
,求 ;
;
(Ⅱ)若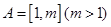 ,且
,且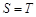 ,求实数m的值.
,求实数m的值.
已知椭圆 ,椭圆的右焦点为F.
,椭圆的右焦点为F.
(1)求过点F且斜率为1的直线被椭圆截得的弦长.
(2)求以M(1,1)为中点的椭圆的弦所在的直线方程.
(3)过椭圆的右焦点F的直线l交椭圆于A,B,求弦 AB的中点P的轨迹方程.
已知正四棱柱 中,
中,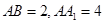 .
.
(Ⅰ)求证: ;
;
(Ⅱ)求钝二面角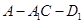 的余弦值;
的余弦值;
(Ⅲ)在线段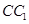 上是否存在点
上是否存在点 ,使得平面
,使得平面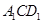
 平面
平面 ,若存在,求出
,若存在,求出 的值;若不存在,
的值;若不存在,
请说明理由.