设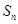 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的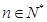 ,都有
,都有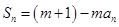
 为常数,且
为常数,且 .
.
(1)求证:数列 是等比数列;
是等比数列;
(2)设数列 的公比
的公比 ,数列
,数列 满足
满足
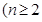 ,
,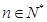
 ,求数列
,求数列 的通项公式;
的通项公式;
(3)在满足(2)的条件下,求数列 的前
的前 项和
项和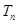 .
.
设二次函数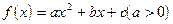 ,方程
,方程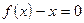 的两个根
的两个根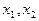 满足
满足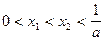 .且函数
.且函数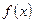 的图像关于直线
的图像关于直线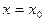 对称,证明:
对称,证明: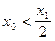 .
.
已知a、b、c是实数,函数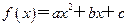 ,
,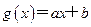 ,当
,当 时,
时, .
.
(1)证明: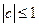 ;
;
(2)证明:当 时,
时,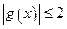 ;
;
一个小服装厂生产某种风衣,月销售量x(件)与售价P(元/件)之间的关系为P=160-2x,生产x件的成本R=500+30x元.
(1)该厂的月产量多大时,月获得的利润不少于1300元?
(2)当月产量为多少时,可获得最大利润?最大利润是多少元?
二次函数f(x)=px2+qx+r中实数p、q、r满足 =0,其中m>0,求证:
=0,其中m>0,求证:
(1)pf( )<0;
)<0;
(2)方程f(x)=0在(0,1)内恒有解.
如果二次函数y=mx2+(m-3)x+1的图象与x轴的交点至少有一个在原点的右侧,试求m的取值范围.