某公司有甲种原料260kg，乙种原料270kg，计划用这两种原料生产A、B两种产品共40件．生产每件A种产品需甲种原料8kg，乙种原料5kg，可获利润900元；生产每件B种产品需甲种原料4kg，乙种原料9kg，可获利润1100元．设安排生产A种产品x件．
（1）完成下表
| |
甲（kg） |
乙（kg） |
件数（件） |
| A |
|
5x |
x |
| B |
4（40-x） |
|
40-x |
（2）安排生产A、B两种产品的件数有几种方案？试说明理由；
（3）设生产这批40件产品共可获利润y元，将y表示为x的函数，并求出最大利润．
如图，有一个面积为150㎡的长方形鸡场，鸡场的一边靠墙（墙长18,米），墙的对面有一个2米宽的门，另外三边（门除外）用篱笆围成，篱笆总长为33米，求鸡场的长与宽分别是多少？ 
解方程（
（1）、
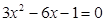（配方法）（2）、
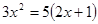（公式法）
某新建住宅小区里，有一块三角形绿地，现准备在其中安装一个照明灯P，使它到绿地各边的距离相等.请你在图中画出安装照明灯P的位置.
结论：
如图，在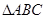
中，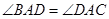
，
，
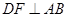，AF=10cm， AC=14cm，动点E以2cm/s的速度从
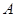点向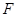
点运动，动点
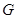以1cm/s的速度从
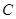点向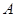点运动，当一个点到达终点时，另一个点随之停止运动，设运动时间为t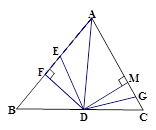
(1)求证：在运动过程中，不管t取何值，都有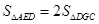
；
(2)当t取何值时，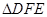
与
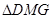全等
如图，在四边形ABCD中，DC∥AB，BD平分∠ADC，∠ADC=60°，过点B作BE⊥DC，过点A作AF⊥BD，垂足分别为E、F，连接EF判断△BEF的形状，并说明理由