如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm．动点M，N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A，B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动，连接PM，PN，设移动时间为t（单位：秒，0＜t＜2.5）．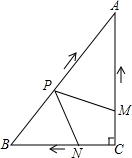
（1）当t为何值时，以A，P，M为顶点的三角形与△ABC相似？
（2）是否存在某一时刻t，使四边形APNC的面积S有最小值？若存在，求S的最小值；若不存在，请说明理由．
（11·大连）（本题12分）如图7，某建筑物BC上有一旗杆AB，小明在与BC
相距12m的F处，由E点观测到旗杆顶部A的仰角为52°、
底部B的仰角为45°，小明的
观测点与地面的距离EF为1.6m．
⑴求建筑物BC的高度；
⑵求旗杆AB的高度．
（结果精确到
0.1m．参考数据
：
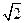≈1.41，sin52°≈0.79，tan52°≈1.28）
（11·大连）（本题9分）如图6，等
腰梯形ABCD中，AD∥BC，M是
BC的中点，求证：∠DAM＝∠ADM．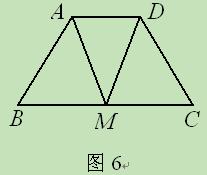
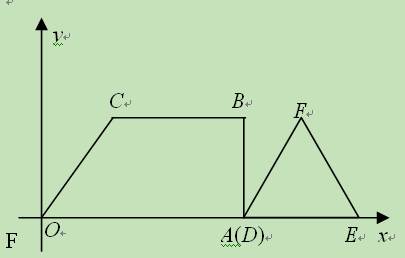
（11·天水）在梯形OABC中，CB∥OA，∠AOC＝60°，∠OAB＝90°，
OC＝2，BC＝4，以点O为原点，OA所在的直线为x轴，建立平面直角坐标系，另有一边
长为2的等边△DEF，DE在x轴上（如图（1）），如果让△DEF以每秒1个单位的速度向
左作匀速直线运动，开始时点D与点A重合，当点D到达坐标原点时运动停止．
（1）设△DEF运动时间为t，△DEF与梯形OABC重叠部分的面积为S，求S关于t的函
数关系式．
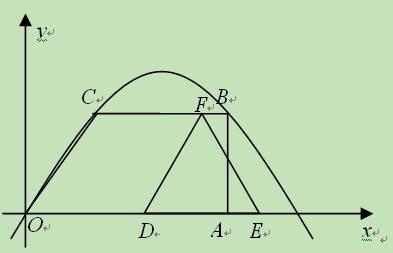
（2）探究：在△DEF运动过程中，如果射线DF交经过O、C、B三点的抛物线于点G，是
否存在这样的时刻t，使得△OAG的面积与梯形OABC的面积相等？若存在，求出t的值；
若不存在，请说明理由．
