正方形ABCD的顶点A在直线MN上,点O是对角线AC、BD的交点,过点O作OE⊥MN于点E,过点B作BF⊥MN于点F.
(1)如图1,当O、B两点均在直线MN上方时,易证:AF+BF=2OE(不需证明)
(2)当正方形ABCD绕点A顺时针旋转至图2、图3的位置时,线段AF、BF、OE之间又有怎样的关系?请直接写出你的猜想,并选择一种情况给予证明.
如图,在平面直角坐标系xOy中,点A的坐标为(﹣2,0),等边三角形AOC经过平移或轴对称都可以得到△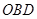 .
.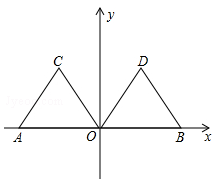
(1)△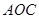 沿x轴向右平移得到△
沿x轴向右平移得到△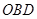 ,则平移的距离是 个单位长度;△
,则平移的距离是 个单位长度;△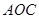 与△
与△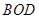 关于直线对称,则对称轴是 ;
关于直线对称,则对称轴是 ;
(2)连结AD,交OC于点E,求∠AEO的度数.
已知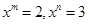 ,求
,求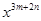 的值.
的值.
已知:如图,AE是△ABC外角的平分线,且AE∥BC.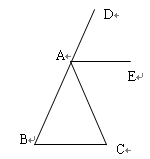
求证:△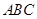 是等腰三角形。
是等腰三角形。
计算:
(1)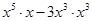
(2)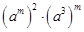 ;
;
(3)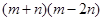
(4)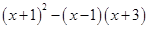
(本题14分)如图,在等边 中,
中, 于点
于点 ,点
,点 在边
在边 上运动,过点
上运动,过点 作
作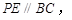 与边
与边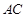 交于点
交于点 ,连结
,连结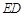 ,以
,以 为邻边作□
为邻边作□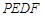 ,设□
,设□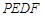 与
与 重叠部分图形的面积为
重叠部分图形的面积为 ,线段
,线段 的长为
的长为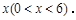
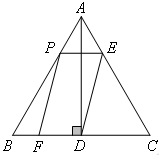
(1)求线段 的长(用含
的长(用含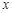 的代数式表示);
的代数式表示);
(2)当四边形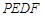 为菱形时,求
为菱形时,求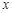 的值;
的值;
(3)直接写出 与
与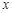 之间的函数关系式.
之间的函数关系式.