如图,椭圆的中心为原点O,长轴在x轴上,离心率e=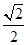
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,
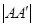=4.
(1)求该椭圆的标准方程;
(2)取平行于y轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.求△PP′Q的面积S的最大值,并写出对应的圆Q的标准方程.
已知，如图四棱锥P—ABCD中，底面ABCD是平行四边形，PG⊥平面ABCD，垂足为G，G在AD上，且AG=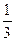
GD，BG⊥GC，GB=GC=2，E是BC的中点，四面体P—BCG的体积为
．
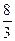（Ⅰ）求异面直线GE与PC所成的角；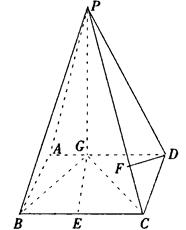
（Ⅱ）求点D到平面PBG的距离；
（Ⅲ）若F点是棱PC上一点，且DF⊥GC，求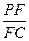
的值．
已知一台机器在一天内发生故障的概率为0．2，机器发生故障时全天停止工作．一周五天工作日里无故障可获利10万元，发生一次故障可获利5万元，发生两次故障没有利润，发生三次或三次以上故障就要亏损2万元．这台机器在一周内平均获利多少？
已知某厂生产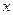
件产品的成本为
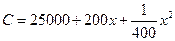（元），问：（1）要使平均成本最低，应生产多少件产品？（2）若产品以每件
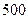元售出，要使利润最大，应生产多少件产品？
一火车每小时煤消耗的费用与火车行驶的速度之立方成正比，已知当速度为每小时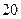
千米时，每小时消耗煤之价格为
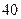元，其他费用每小时要
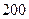元，问火车行驶的速度如何时，才能使火车从甲城开往乙城的费用最少。（已知火车的最高速度为每小时
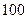千米）
最初质量为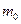
的水滴，在重力的作用下下落，由于蒸发而减少质量，并且减少的质量与时间成正比（比例常数为
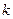），从它下落开始经过多少秒时，动能达到最大？动能的最大值为多少？