已知直线l: +4-3m=0.
+4-3m=0.
(1)求证:不论m为何实数,直线l恒过一定点M;
(2)过定点M作一条直线l1,使夹在两坐标轴之间的线段被M点平分,求直线l1的方程.
(本小题满分14分)设锐角三角形ABC的内角A,B,C的对边分别为 ,
,
(Ⅰ)求B的大小;
(Ⅱ)求 的取值范围
的取值范围
(本小题满分14分)已知向量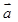 =(
=( ,1),向量
,1),向量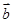 =(sin2x,cos2x),函数
=(sin2x,cos2x),函数
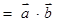
(1)求函数 的表达式,并作出函数
的表达式,并作出函数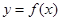 在一个周期内的简图(用五点法列表描点);
在一个周期内的简图(用五点法列表描点);
(2)求函数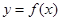 的周期,并写单调区间.
的周期,并写单调区间.
(本小题满分10分)若数列 的前n项和为
的前n项和为 ,且方程
,且方程 有一个根为
有一个根为 -1,n=1,2,3...
-1,n=1,2,3...
(1)求 ;
;
(2)猜想数列 的通项公式,并用数学归纳法证明
的通项公式,并用数学归纳法证明
(本小题满分10分)已知直三棱柱 中,
中, ,
, 是棱
是棱 的中点.如图所示.
的中点.如图所示.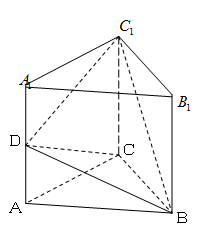
(1)求证: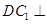 平面
平面 ;
;
(2)求锐二面角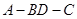 的大小.
的大小.
(本小题满分10分)已知圆C的极坐标方程为 =2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,若直线
=2,以极点为原点,极轴为x轴的正半轴建立平面直角坐标系,若直线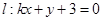 与圆C相切.
与圆C相切.
求(1)圆C的直角坐标方程;
(2)实数k的值.