解下列分式方程:
(1)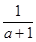 +
+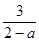 =0;
=0;
(2)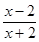 -
-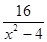 =
=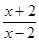 .
.
如图:E在△ABC的AC边的延长线上,D点在AB边上,DE交BC于点F,DF=EF,BD="CE," 过D作DG∥AC交BC于G.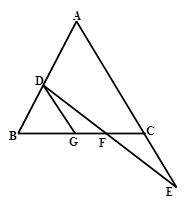
求证:(1) △GDF≌△CEF;
(2)△ABC是等腰三角形.
如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1) AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何? 说明理由.
(3)BC平分∠DBE吗? 说明理由.
为增强中学生体质,开展了“每天锻炼一小时”的体育活动.4月份对全市中小学生进行体质监测评价,专家组随机抽查了某区若干名初中学生. 我们对专家的测评数据作了适当处理,并将统计结果绘制了如下两幅不完整的统计图,请你根据图中所给信息解答下列问题:
(1)在这次监测评价中,一共抽查了名学生,如果全市有10万名初中生,那么全市初中生中,可以达到优秀的学生约有人;
(2)请将两幅统计图补充完整.(补全直方图及数据)
良好人数;
良好率;
不及格率.
已知△ABC的三边 满足
满足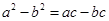 ,试判断△ABC的形状.
,试判断△ABC的形状.
如图,在正方形网格上的一个△ABC.
(1)作△ABC关于直线MN的对称图形(不写作法);
(2)以P为一个顶点作与△ABC全等的三角形(规定点P与点B对应,另两顶点都在图中网格交点处),则可作出个三角形.