已知函数f(x)=(x-a)2(x-b)(a,b∈R,a<b).
(1)当a=1,b=2时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(2)设x1,x2是f(x)的两个极值点,x3是f(x)的一个零点,且x3≠x1,x3≠x2.证明:存在实数x4,使得x1,x2,x3,x4按某种顺序排列后构成等差数列,并求x4.
（本小题满分12分）
如图，在三棱锥P－ABC中，PA＝PC，∠APC＝∠ACB＝90°，∠BAC＝30°，平面PAC⊥平面ABC．
（1）求证：平面PAB⊥平面PBC；
（2）若PA＝2，求三棱锥P－ABC的体积．
（本小题满分10分）
7名学生站成一排，下列情况各有多少种不同的排法?
(1)甲、乙必须排在一起；
(2)甲不在排头，乙不在排尾；
(3)甲、乙互不相邻；
(4)甲、乙之间须隔一人
（本题满
分12分）
已知函数f(x)=A
(A>0,
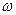>0,0<
<
函数，且y=f
(x)的最大值为2，其图象相邻两对称轴间的距离为2，并过点（1，2）.
（1）求;
（2）计算f(1)+f(2)+… +f(2 008).
已知函数
，
.求:
(I) 函数
的最大值及取得最大值的自变量
的集合；
(II) 函数的单调增区间.
如图为函数y=Asin(ωx
+φ)(A＞0,ω＞0)的图象的一部分，试求该函数的一个解析式.