如图,圆O1与圆O2的半径都是1,O1O2=4,过动点P分别作圆O1、圆O2的切线PM、PN(M、N分别为切点),使得PM=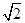 PN,试建立适当的坐标系,并求动点P的轨迹方程.
PN,试建立适当的坐标系,并求动点P的轨迹方程.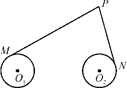
已知函数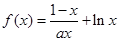 .
.
(Ⅰ)若函数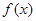 在
在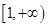 上是增函数,求正实数
上是增函数,求正实数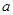 的取值范围;
的取值范围;
(Ⅱ)若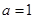 ,
,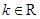 且
且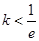 ,设
,设 ,求函数
,求函数 在
在 上的最大值和最小值.
上的最大值和最小值.
已知椭圆 :
: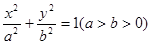 的右焦点
的右焦点 ,过原点和
,过原点和 轴不重合的直线与椭圆
轴不重合的直线与椭圆 相交于
相交于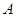 ,
, 两点,且
两点,且 ,
, 最小值为
最小值为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)若圆: 的切线
的切线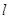 与椭圆
与椭圆 相交于
相交于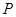 ,
, 两点,当
两点,当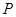 ,
, 两点横坐标不相等时,问:
两点横坐标不相等时,问: 与
与 是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
是否垂直?若垂直,请给出证明;若不垂直,请说明理由.
如图,在直三棱柱 中,平面
中,平面 侧面
侧面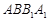 .
.
(Ⅰ)求证: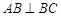 ;
;
(Ⅱ)若直线 与平面
与平面 所成角是
所成角是 ,锐二面角
,锐二面角 的平面角是
的平面角是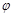 ,试判断
,试判断 与
与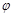 的大小关系,并予以证明.
的大小关系,并予以证明.
设Sn是正项数列 的前n项和,
的前n项和,  .
.
(I)求数列 的通项公式;
的通项公式;
(II)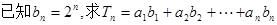 的值.
的值.
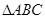 的三个内角
的三个内角 所对的边分别为
所对的边分别为 ,向量
,向量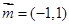 ,
,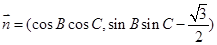 ,且
,且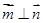 .
.
(Ⅰ)求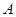 的大小;
的大小;
(Ⅱ)现在给出下列三个条件:1、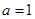 ;2、
;2、 ;3、
;3、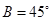 ,试从中再选择两个条件以确定
,试从中再选择两个条件以确定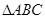 ,求出所确定的
,求出所确定的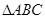 的面积.
的面积.
(注:只需要选择一种方案答题,如果用多种方案答题,则按第一方案给分).