如图,三棱锥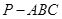 中,
中, ,
,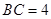 ,
,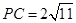 ,点
,点 在平面
在平面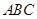 内的射影恰为
内的射影恰为 的重心
的重心 ,M为侧棱
,M为侧棱 上一动点.
上一动点.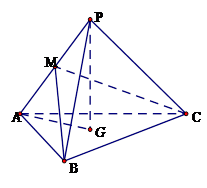
(1)求证:平面 平面
平面 ;
;
(2)当M为 的中点时,求直线
的中点时,求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
中央电视台《同一首歌》大型演唱会曾在厦门举行,之前甲、乙两人参加大会青年志愿者的选拔.已知在备选的10道试题中,甲能答对其中的6题,乙能答对其中的8题。规定每次考试都从备选题中随机抽出3题进行测试,至少答对2题才能入选。
(Ⅰ)求甲答对试题数ξ的概率分布 (列表);
(列表);
(Ⅱ)求甲、乙两人至少有一人入选的概率。
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD.SD=2,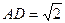 ,E是SD上的点。
,E是SD上的点。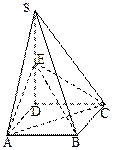
(Ⅰ)求证: AC⊥BE;
AC⊥BE;
(Ⅱ)求二面角C—AS—D的余弦值。
(本小题满分12分)已知函数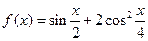
(1)求函数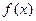 的最小正周期;
的最小正周期;
(2)在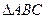 中,角
中,角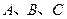 的分别是
的分别是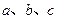 ,若
,若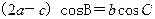 ,求
,求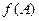 的取值范围
的取值范围
(本小题满分14分)已知函数f(x)=ln(x+a)-x2-x在x = 0处取得极值.
(Ⅰ)求实数a的值;
(Ⅱ)若关于x的方程,f(x)= 在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
在区间[0,2]上恰有两个不同的实数根,求实数b的取值范围;
(Ⅲ)证明:对任意的正整数n,不等式ln 都成立.
都成立.
(本小题满分12分)已知椭圆C: 过点
过点 ,且长轴长等于4.
,且长轴长等于4.
(Ⅰ)求椭圆C的方程;
(Ⅱ) 是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若
是椭圆C的两个焦点,⊙O是以F1F2为直径的圆,直线l: y=kx+m与⊙O相切,并与椭圆C交于不同的两点A、B,若 ,求
,求 的值
的值