如图,在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2。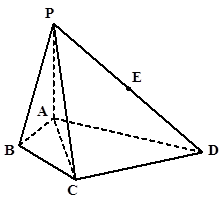
(1)求证:CE∥平面PAB;
(2)求四面体PACE的体积.
在△ABC中,角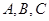 所对的边分别是
所对的边分别是 ,且
,且 。
。
(1)求 的值;
的值;
(2)若 ,
,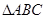 的面积
的面积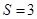 ,求
,求 的值.
的值.
已知α为锐角,且sin α=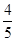 .
.
(1)求 的值;
的值;
(2)求tan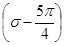 的值.
的值.
函数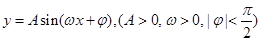 的最小值是
的最小值是 ,在一个周期内图象最高点与最低点横坐标差是
,在一个周期内图象最高点与最低点横坐标差是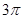 ,又:图象过点
,又:图象过点 ,
,
求(1)函数解析式,
(2)函数的最大值、以及达到最大值时 的集合;
的集合;
袋中装着分别标有数字1,2,3,4,5的5个形状相同的小球.
(1)从袋中任取2个小球,求两个小球所标数字之和为3的倍数的概率;
(2)从袋中有放回的取出2个小球,记第一次取出的小球所标数字为x,第二次为y,求满足|x-y|>2或x+y>7的概率.
已知 ,
,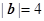 ,且向量
,且向量 与
与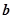 不共线.
不共线.
(1)若 与
与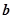 的夹角为
的夹角为 ,求
,求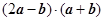 ;
;
(2)若向量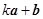 与
与 互相垂直,求
互相垂直,求 的值.
的值.