如图所示,光滑固定的竖直杆上套有一个质量m=0.4 kg的小物块A,不可伸长的轻质细绳通过固定在墙壁上、大小可忽略的定滑轮D,连接小物块彳和小物块曰,虚线CD水平,间距d=1.2 m,此时连接小物块彳的细绳与竖直杆的夹角为37°,小物块彳恰能保持静止.现在在小物块B的下端挂一个小物块Q(未画出,小物块A可从图示位置上升并恰好能到达C处,不计摩擦和空气阻力,cos37°= 0.8、sin37°=0.6,重力加速度誊取l0m/s2.求:
(1)小物块A到达C处时的加速度大小;
(2)小物块B的质量;
(3)小物块Q的质量.
有一玻璃半球,右侧面镀银,光源S就在其对称轴SO上(O为球心),且SO水平,如右图所示。从光源S发出的一束光射到球面上,其中一部分光经球面反射后恰能竖直向上传播,另一部分光折入玻璃半球内,经右侧镀银面第一次反射恰能沿原路返回。若球面半径为R,玻璃折射率为 ,求光源S与球心O之间的距离SO为多大?
,求光源S与球心O之间的距离SO为多大?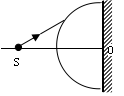
光滑水平面AB与竖直面内的粗糙半圆形导轨在B点平滑连接,导轨半径为R,一个质量m的小物块在A点以v0=3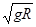 的速度向B点运动,如图所示, AB=4R,物块沿圆形轨道通过最高点C后做平抛运动,最后恰好落回出发点A。( g取10 m/s2),求:
的速度向B点运动,如图所示, AB=4R,物块沿圆形轨道通过最高点C后做平抛运动,最后恰好落回出发点A。( g取10 m/s2),求: 
(1) 物块在C点时的速度大小vC;
(2) 物块在C点处对轨道的压力大小FN;
(3) 物块从B到C过程阻力所做的功。
如图所示,一质量为m的物块从光滑斜面顶端的A点由静止开始下滑,A点到水平地面BC的高度H=2m,通过水平地面BC(BC=2m)后滑上半径为R=1m的光滑1/4圆弧面CD,上升到D点正上方0.6m(图中未画出最高点)后又再落下。(设各轨道连接处均平滑且物块经过时无能量损失, g取10 m/s2)。求:
(1)物块第一次到达B点时的速度vB;
(2)物块第一次从B到C克服阻力所做的功;
(3)物块最终停在距B点右侧多远处?
太阳系外行星大多不适宜人类居住,绕恒星“Glicsc581”运行的行星“Gl-581c” 却很值得我们期待。该行星的温度在0℃到40℃之间,质量是地球的6倍,直径是地球的1.5倍、公转周期为13个地球日。“Glicsc581”的质量是太阳质量的0.31倍。设该行星与地球均视为质量分布均匀的球体,绕其中心天体做匀速圆周运动,则求:
(1).如果人到了该行星,其体重是地球上的体重的多少倍?
(2).该行星与“Glicsc581”的距离是日地距离的多少倍?(结果不用整理到最简,可带小数和根号)
质量为m =5×103 kg的汽车,在t=0 时刻速度v0=10 m/s,随后以P=6×104 W的额定功率沿平直公路继续前进,经t="72" s达到最大速度。该汽车所受恒定阻力是其重力的0.05倍,取g = 10m/s2,求:
(1)汽车的最大速度vm;
(2)汽车在72 s内经过的路程s。