如图,在平面直角坐标系xOy中,已知F1,F2分别是椭圆E: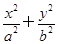 =1(a>b>0)的左、右焦点,A,B分别是椭圆E的左、右顶点,且
=1(a>b>0)的左、右焦点,A,B分别是椭圆E的左、右顶点,且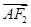 +5
+5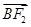 =0.
=0.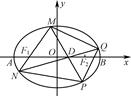
(1)求椭圆E的离心率; (2)已知点D(1,0)为线段OF2的中点,M为椭圆E上的动点(异于点A、B),连结MF1并延长交椭圆E于点N,连结MD、ND并分别延长交椭圆E于点P、Q,连结PQ,设直线MN、PQ的斜率存在且分别为k1、k2,试问是否存在常数λ,使得k1+λk2=0恒成立?若存在,求出λ的值;若不存在,说明理由.
(本小题满分12分)已知向量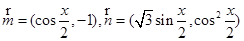 ,设函数
,设函数
(Ⅰ)求 在区间
在区间 上的零点;
上的零点;
(Ⅱ)若角 是△
是△ 中的最小内角,求
中的最小内角,求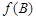 的取值范围.
的取值范围.
(本小题满分14分) 设函数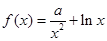 ,
,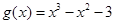 .
.
(Ⅰ)讨论函数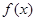 的单调性;
的单调性;
(Ⅱ)若存在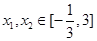 ,使得
,使得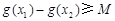 成立,求满足条件的最大整数
成立,求满足条件的最大整数 ;
;
(Ⅲ)如果对任意的 ,都有
,都有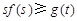 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(本小题满分13分)如图,已知圆E: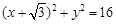 ,点
,点 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.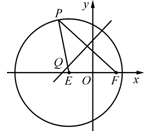
(Ⅰ)求动点Q的轨迹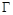 的方程;
的方程;
(Ⅱ)设直线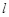 与(Ⅰ)中轨迹
与(Ⅰ)中轨迹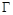 相交于
相交于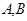 两点, 直线
两点, 直线 的斜率分别为
的斜率分别为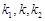 (其中
(其中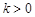 ).△
).△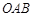 的面积为
的面积为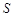 , 以
, 以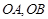 为直径的圆的面积分别为
为直径的圆的面积分别为 .若
.若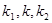 恰好构成等比数列, 求
恰好构成等比数列, 求 的取值范围.
的取值范围.
(本小题满分12分)某创业投资公司拟投资开发某种新能源产品,估计能获得投资收益的范围是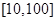 (单位:万元).现准备制定一个对科研课题组的奖励方案:奖金
(单位:万元).现准备制定一个对科研课题组的奖励方案:奖金 (单位:万元)随投资收益
(单位:万元)随投资收益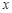 (单位:万元)的增加而增加,且奖金不超过
(单位:万元)的增加而增加,且奖金不超过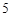 万元,同时奖金不超过投资收益的20%.
万元,同时奖金不超过投资收益的20%.
(Ⅰ)若建立函数模型 制定奖励方案,请你根据题意,写出奖励模型函数应满足的条件;
制定奖励方案,请你根据题意,写出奖励模型函数应满足的条件;
(Ⅱ)现有两个奖励函数模型: ;
;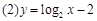 .试分析这两个函数模型是否符合公司要求.
.试分析这两个函数模型是否符合公司要求.
(本小题满分12分)如图,在四棱锥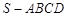 中,底面
中,底面 是正方形,
是正方形, 底面
底面 ,
, , 点
, 点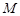 是
是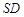 的中点,
的中点,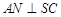 ,且交
,且交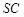 于点
于点 .
.
(Ⅰ)求证: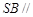 平面
平面 ;
;
(Ⅱ)求证:平面 ⊥平面
⊥平面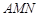 ;
;
(Ⅲ)求二面角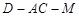 的余弦值.
的余弦值.