一个圆柱形圆木的底面半径为1m,长为10m,将此圆木沿轴所在的平面剖成两个部分.现要把其中一个部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形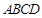 (如图所示,其中O为圆心,
(如图所示,其中O为圆心,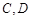 在半圆上),设
在半圆上),设 ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).
(1)求V关于θ的函数表达式;
(2)求 的值,使体积V最大;
的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
已知抛物线 上点
上点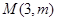 到焦点
到焦点 的距离为4.
的距离为4.
(1)求抛物线方程;
(2)点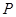 为准线上任意一点,
为准线上任意一点,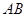 为抛物线上过焦点的任意一条弦(如图),设直线
为抛物线上过焦点的任意一条弦(如图),设直线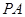 ,
,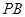 ,
,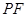 的斜率为
的斜率为 ,
,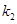 ,
,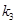 ,问是否存在实数
,问是否存在实数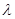 ,使得
,使得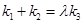 恒成立.若存在,请求出
恒成立.若存在,请求出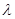 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.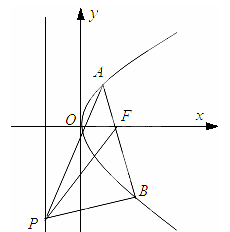
如图,四棱锥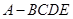 ,平面
,平面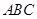 ⊥平面
⊥平面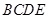 ,△
,△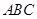 是边长为2的等边三角形,底面
是边长为2的等边三角形,底面 是矩形,且
是矩形,且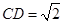 .
.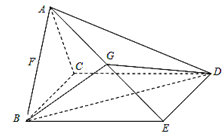
(1)若点 是
是 的中点,求证:
的中点,求证: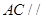 平面
平面 ;
;
(2)若 为
为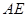 上任意一点,试问点
上任意一点,试问点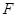 在线段
在线段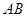 上什么位置时,
上什么位置时,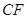 ⊥
⊥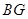 ;
;
(3)若点 是
是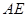 的中点,求
的中点,求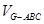 .
.
在数学趣味知识培训活动中,甲乙两名学生的5次培训成绩如茎叶图所示: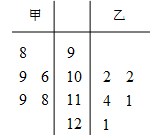
(1)从甲、乙两人中选择1人参加数学趣味知识竞赛,你会选哪位?请运用统计学的知识说明理由;
(2)从乙的5次培训成绩中随机选择2个,试求选到121分的概率.
在等差数列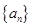 中,
中,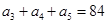 ,
,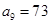 .
.
(1)求数列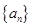 的通项公式;
的通项公式;
(2)对任意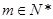 ,将数列
,将数列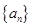 中落入区间
中落入区间 内的项的个数记为
内的项的个数记为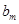 ,求数列
,求数列 的前
的前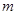 项和
项和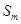 .
.
已知定义域为R的函数f(x)= 是奇函数.
是奇函数.
(1)求a,b的值;
(2)若对任意的t∈R,不等式f(t2-2t)+f(2t2-k)<0恒成立,求k的取值范围.