已知函数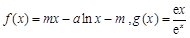 ,其中m,a均为实数.
,其中m,a均为实数.
(1)求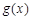 的极值;
的极值;
(2)设 ,若对任意的
,若对任意的
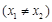 ,
, 恒成立,求
恒成立,求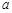 的最小值;
的最小值;
(3)设 ,若对任意给定的
,若对任意给定的 ,在区间
,在区间 上总存在
上总存在 ,使得
,使得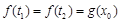 成立,求
成立,求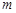 的取值范围.
的取值范围.
(本小题满分13分)
已知函数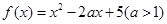 .
.
(1) 若函数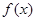 的定义域和值域均为
的定义域和值域均为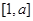 ,求实数
,求实数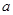 的值;
的值;
(2) 若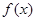 在区间
在区间 上是减函数,且对任意的
上是减函数,且对任意的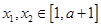 ,
,
总有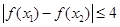 ,求实数
,求实数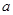 的取值范围;
的取值范围;
(3) 若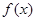 在
在 上有零点,求实数
上有零点,求实数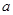 的取值范围.
的取值范围.
(本小题满分12分)
已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为 元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若
元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若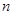 天购买一次,需要支付
天购买一次,需要支付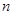 天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
(1)当9天购买一次配料时,求该厂用于配料的保管费用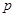 是多少元?[
是多少元?[
(2)设该厂 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这 天中用于配料的总费用
天中用于配料的总费用 (元)关于
(元)关于 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
(本小题满分12分)
已知函数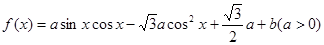
(1)求函数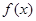 的单调递减区间;
的单调递减区间;
(2)设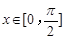 ,
,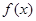 的最小值是
的最小值是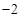 ,最大值是
,最大值是 ,求实数
,求实数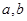 的值.
的值.
(本小题满分12分)
已知实数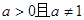 ,命题
,命题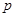 :
: 在区间
在区间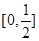 上为减函数;命题
上为减函数;命题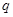 :方程
:方程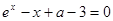 在
在 有解。若
有解。若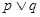 为真,
为真,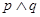 为假,求实数
为假,求实数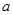 的取值范围。
的取值范围。
(本小题满分12分)
在△ABC中,设角A、B、C的对边分别为a、b、c,且 .
.
(1)求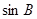 的值;
的值;
(2)若 ,且
,且 ,求△ABC的面积.
,求△ABC的面积.