(本小题满分12分)
已知某食品厂需要定期购买食品配料,该厂每天需要食品配料200千克,配料的价格为 元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若
元/千克,每次购买配料需支付运费236元.每次购买来的配料还需支付保管费用(若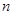 天购买一次,需要支付
天购买一次,需要支付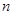 天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
天的保管费)。其标准如下: 7天以内(含7天),无论重量多少,均按10元/天支付;超出7天以外的天数,根据实际剩余配料的重量,以每天0.03元/千克支付.
(1)当9天购买一次配料时,求该厂用于配料的保管费用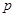 是多少元?[
是多少元?[
(2)设该厂 天购买一次配料,求该厂在这
天购买一次配料,求该厂在这 天中用于配料的总费用
天中用于配料的总费用 (元)关于
(元)关于 的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
的函数关系式,并求该厂多少天购买一次配料才能使平均每天支付的费用最少?
如图,设抛物线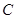 :
: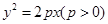 的焦点为
的焦点为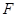 ,准线为
,准线为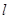 ,过准线
,过准线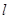 上一点
上一点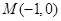 且斜率为
且斜率为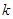 的直线
的直线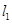 交抛物线
交抛物线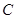 于
于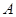 ,
,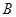 两点,线段
两点,线段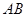 的中点为
的中点为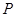 ,直线
,直线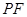 交抛物线
交抛物线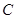 于
于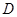 ,
,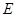 两点.
两点.
(1)求抛物线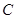 的方程及
的方程及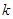 的取值范围;
的取值范围;
(2)是否存在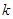 值,使点
值,使点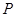 是线段
是线段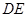 的中点?若存在,求出
的中点?若存在,求出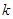 值,若不存在,请说明理由.
值,若不存在,请说明理由. 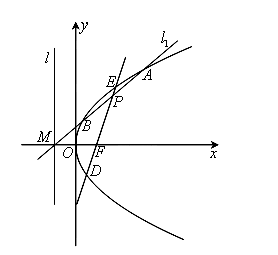
如图,三棱柱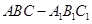 是直棱柱,
是直棱柱,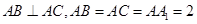 .点
.点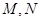 分别为
分别为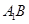 和
和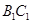 的中点.
的中点. 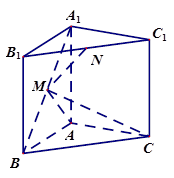
(1)求证: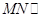 平面
平面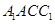 ;
;
(2)求点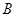 到平面
到平面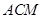 的距离.
的距离.
节日期间,高速公路车辆较多,某调查公司在一服务区从七座以下小型汽车中按进服务区的顺序,随机抽取第一辆汽车后,每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速(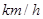 )分成六段
)分成六段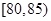 ,
,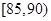 ,
,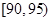 ,
,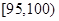 ,
,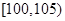 ,
,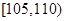 后得到如下图的频率分布直方图.
后得到如下图的频率分布直方图.
(1)请直接回答这种抽样方法是什么抽样方法?并估计出这40辆车速的中位数;
(2)设车速在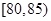 的车辆为
的车辆为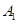 ,
,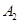 , ,
, ,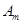 (
(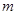 为车速在
为车速在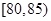 上的频数),车速在
上的频数),车速在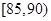 的车辆为
的车辆为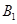 ,
,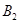 , ,
, ,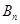 (
(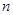 为车速在
为车速在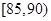 上的频数),从车速在
上的频数),从车速在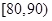 的车辆中任意抽取
的车辆中任意抽取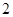 辆共有几种情况?请列举出所有的情况,并求抽取的
辆共有几种情况?请列举出所有的情况,并求抽取的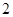 辆车的车速都在
辆车的车速都在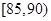 上的概率.
上的概率.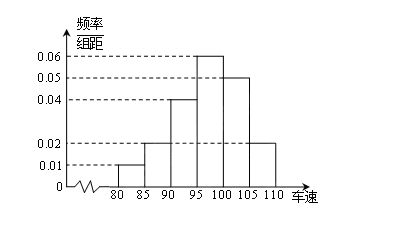
已知函数 (
(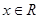 ).
).
(1)求 的单调递增区间;
的单调递增区间;
(2)在锐角三角形 中,
中, 、
、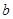 、
、 分别是角
分别是角 、
、 、
、 的对边,若
的对边,若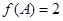 ,
, ,
,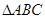 的面积为
的面积为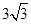 ,求
,求 的值.
的值.
设数列 满足
满足 ,且对任意
,且对任意 ,函数
,函数

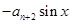 满足
满足 ,若
,若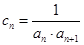 ,则数列
,则数列 的前
的前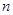 项和
项和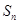 为.
为.