电解槽A和电炉B并联后接到电源上,电源内阻r=1 Ω,电炉电阻R=19 Ω,电解槽电阻r0=0.5 Ω.当S1闭合、S2断开时,电炉消耗功率为684 W;S1、S2都闭合时电炉消耗功率为475 W(电炉电阻可看作不变).试求:
(1)电源的电动势;
(2)S1、S2闭合时,流过电解槽的电流大小;
(3)S1、S2闭合时,电解槽中电能转化成化学能的功率.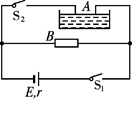
如图所示,质量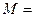 20kg的物体从光滑曲面上高度
20kg的物体从光滑曲面上高度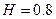 m处释放,到达底端时水平进入水平传送带,传送带由一电动机驱动着匀速向左转动,速率恒为3m/s.已知物体与传送带间的动摩擦因数
m处释放,到达底端时水平进入水平传送带,传送带由一电动机驱动着匀速向左转动,速率恒为3m/s.已知物体与传送带间的动摩擦因数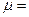 0.1.(g取10m/s2)
0.1.(g取10m/s2)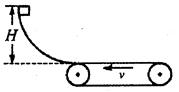
若两皮带轮之间的距离是6m,物体冲上传送带后就移走光滑曲面,物体将从哪一边离开传送带?通过计算说明你的结论.
若皮带轮间的距离足够大,从M滑上到离开传送带的整个过程中,由于M和传送带间的摩擦而产生了多少热量?
天文学家将相距较近、仅在彼此的引力作用下运行的两颗恒星称为双星,双星系统在银河系中很普遍。利用双星系统中两颗恒星的运动特征可推算出它们的总质量。已知某双星系统中两颗恒星围绕它们连线上的某一固定点分别做匀速圆周运动,周期均为T,两颗恒星之间的距离为r,试推算这个双星系统的总质量。(引力常量为G)
某型号小汽车发动机的额定功率为60 kW,汽车质量为1×103 kg,在水平路面上正常行驶中所受到的阻力为车重的0.15倍,g取10 m/s2.求:此型号汽车在水平路面行驶能达到的最大速度是多少?
若此型号汽车以额定功率加速行驶,当速度达到20 m/s 时的加速度大小是多少?
质量为60 kg的驾驶员驾驶此型号汽车在水平高速公路上以30 m/s的速度匀速行驶,设轮胎与路面的动摩擦因数为0.60,驾驶员的反应时间为0.30 s,则驾驶员驾驶的汽车与前车保持的安全距离最少为多少?
如图所示电子射线管.阴极K发射电子,阳极P和阴极K间 加上电压后电子被加速。A、B是偏向板,使飞进的电子偏离.若已知P、K间所加电压UPK=2.5×103V,两极板长度L=6.0×10-2m,板间距离d=3.6×10-2m,所加电压UAB=1000V,R=3×10-2m, 电子质量me=9.1×10-31kg,电子的电荷量e=-1.6×10-19C。设从阴极出来的电子速度为0,不计重力。 试问:电子通过阳极P板的速度υ0是多少?
电子通过偏转电极时具有动能Ek是多少?
电子过偏转电极后到达距离偏转电极R=3×10-2m荧光屏上 O′点,此点偏离入射方向的距离y是多少?
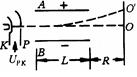
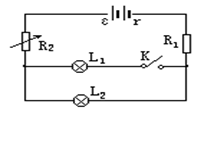
如图所示的电路中已知电源电动势E=36V,内电阻r=2Ω,R1=20Ω,每盏灯额定功率都是2W,额定电压也相同。当K闭合调到R2=14Ω时,两灯都正常发光;当K断开后为使L2仍正常发光,求R2应调到何值?